Bestimmen Sie anhand des Graphen der Funktion \(V\) näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn.
(3 BE)
Lösung zu Teilaufgabe 2b
Graphische Bestimmung der momentanen Änderungsrate einer Funktion
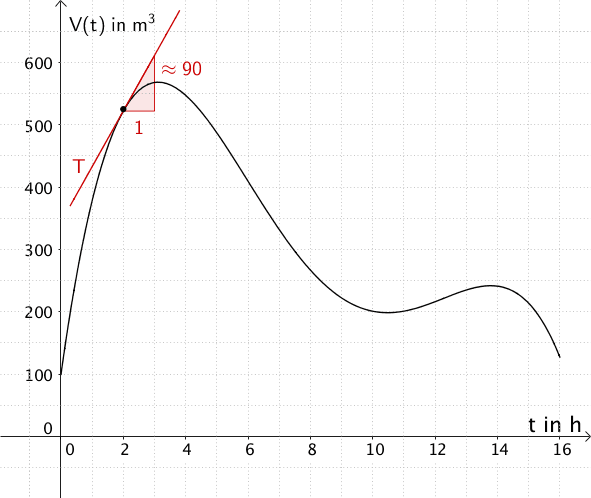
Die Steigung der Tangente \(T\) an den Graphen der Funktion \(V\) zum Zeitpunkt \(t = 2\) entspricht der momentanen Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn (Einheit: \(\frac{\sf{m^{3}}}{\sf{h}}\)).
Differentialquotient oder lokale bzw. momentane Änderungsrate
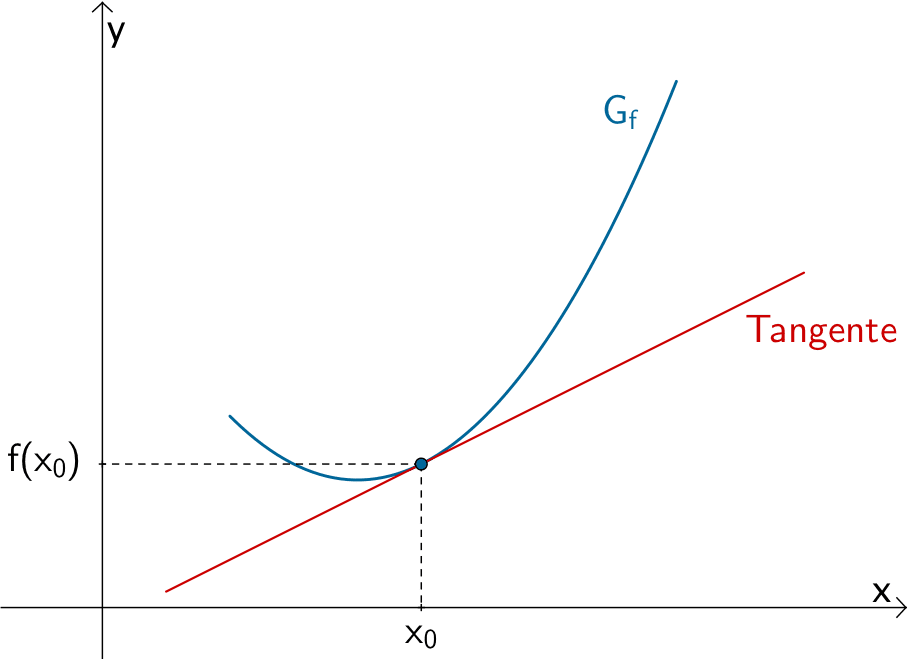
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\[m_{T} \approx \frac{90}{1} = 90\]
Die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn beträgt näherungsweise \(90\,\frac{\sf{m^{3}}}{\sf{h}}\).


