Die Abbildung zeigt einen Ausschnitt des Graphen \(G\) der in \(\mathbb R \backslash \{-3\}\) definierten Funktion \(f\) mit \(f(x) = x - 3 + \dfrac{5}{x+3}\). \(G\) hat genau einen Tiefpunkt \(T\).

Die Geraden mit den Gleichungen \(x = -3\) und \(y = x-3\) haben eine besondere Bedeutung für \(G\). Zeichnen Sie die beiden Geraden in die Abbildung ein und geben Sie diese Bedeutung an. Geben Sie zudem die Koordinaten des Schnittpunkts der beiden Geraden an.
(4 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = x - 3 + \dfrac{5}{x+3}\; \; D_f = \mathbb R \backslash \{-3\}\]
Einzeichnen und Bedeutung der beiden Geraden
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{p(x)}{q(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(p(x)\) und \(q(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(q(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
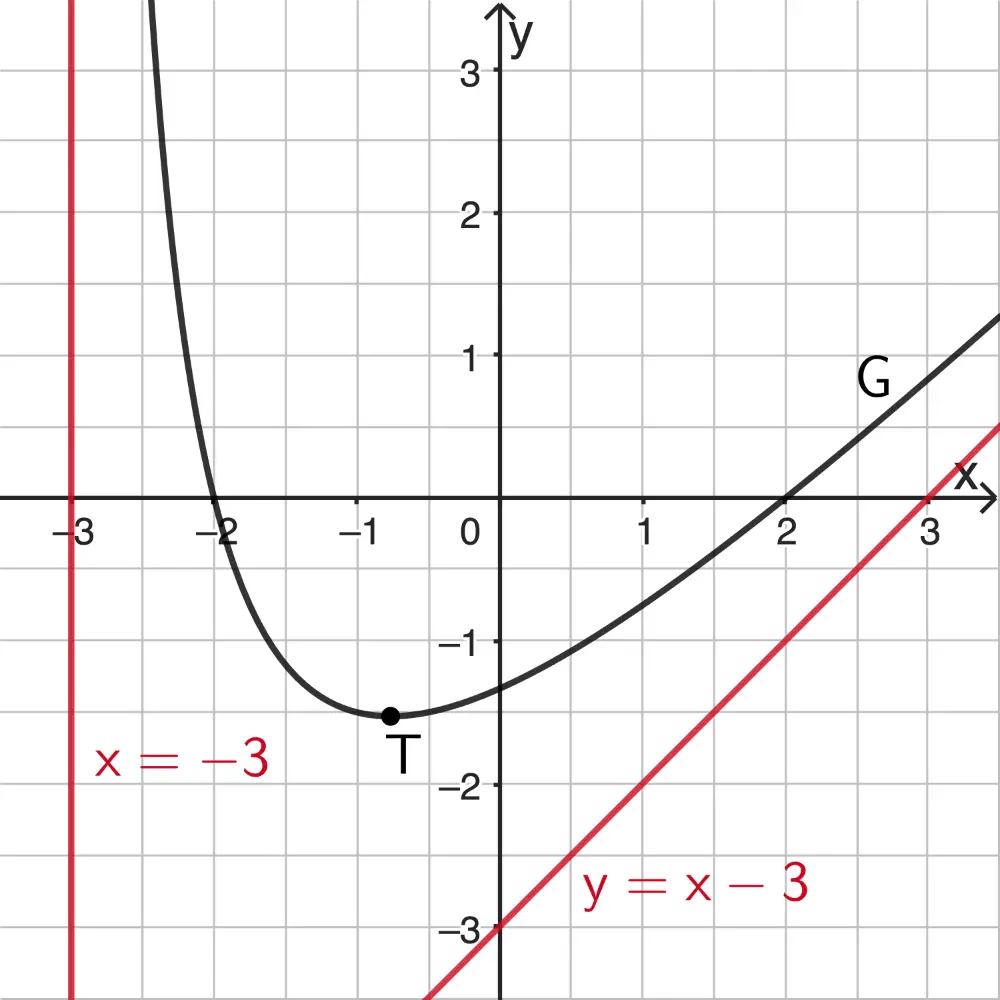
Die Gerade mit der Gleichung \(\textcolor{#cc071e}{x = -3}\) ist senkrechte Asymptote von \(G\) an der Definitionslücke \(x = -3\).
Die Gerade mit der Gleichung \(\textcolor{#cc071e}{y = x-3}\) ist schräge Asymptote von \(G\) für \(x \to \pm \infty\).
Koordinaten des Schnittpunkts der beiden Geraden
Die Gerade mit der Gleichung \(x = -3\) legt die \(x\)-Koordinate des Schnittpunkts fest. \(x = -3\) in die Geradengleichung \(y = x - 3\) eingesetzt, ergibt \(y = -3 - 3 = -6\). Somit besitzen die beiden Geraden den Schnittpunkt \((-3|-6)\).


