Die Inhaberin der Losbude beschäftigt einen Angestellten, der Besucher des Volksfests anspricht, um diese zum Kauf von Losen zu animieren. Sie ist mit der Erfolgsquote des Angestellten unzufrieden.
Die Inhaberin möchte dem Angestellten das Gehalt kürzen, wenn weniger als 15 % der angesprochenen Besucher Lose kaufen. Die Entscheidung über die Gehaltskürzung soll mithilfe eines Signifikanztests auf der Grundlage von 100 angesprochenen Besuchern getroffen werden. Dabei soll möglichst vermieden werden, dem Angestellten das Gehalt zu Unrecht zu kürzen. Geben Sie die entsprechende Nullhypothese an und ermitteln Sie die zugehörige Entscheidungsregel auf dem Signifikanzniveau von 10 %.
(5 BE)
Lösung zu Teilaufgabe 3a
Die Entscheidungsregel wird mithilfe eines Signifikanztests ermittelt. Ein Signifikanztest gibt der Wahrscheinlichkeit für den Fehler 1. Art (Nullhypothese wird irrtümlich abgelehnt) eine Obergrenze vor (Signifikanzniveau). Unter dieser Bedingung können die Grenzen, die den Annahmebereich vom Ablehnungsbereich der Nullhypothese trennen, mithilfe des Stochastischen Tafelwerks bestimmt werden.
Einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\)
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\alpha\) überprüft eine Vermutung, dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Dabei darf die Wahrscheinlichkeit für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreichen.
Linksseitiger Signifikanztest
\[H_0 \colon p_0 \geq p \quad H_1 \colon p_1 < p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{0; 1; ...; k\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
Rechtsseitiger Signifikanztest
\[H_0 \colon p_0 \leq p \quad H_1 \colon p_1 > p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{k + 1; ...; n\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 &&| \textcolor{red}{\cdot (-1)} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
ST: Stochastisches Tafelwerk
1. Nullhypothese benennen
Der Satz „Dabei soll möglichst vermieden werden, dem Angestellten das Gehalt zu Unrecht zu kürzen." beschreibt den Fehler 1. Art, dessen Wahrscheinlichkeit das Signifikanzniveau von 10 % nicht überschreiten soll.
„zu Unrecht" bedeutet im Sachzusammenhang: „obwohl mindestens 15 % der angesprochenen Besucher Lose kaufen."
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\(\Longrightarrow \quad H_{0} \colon p \geq 0{,}15\), („Mindestens 15 % der angesprochenen Besucher kaufen Lose.")
2. Zufallsgröße (Testgröße) einführen
Bei einer Stichprobe von 100 zufällig angesprochenen Besuchern wird auf das Ereignis „Besucher kauft Lose" geachtet. Die Wahrscheinlichkeit für dieses Ereignis ist gemäß der Nullhypothese mit \(p_{0} = 0{,}15\) konstant (vgl. Anmerkung 2).
Es sei \(X\) die Zufallsgröße, welche die Anzahl der angesprochenen Besucher beschreibt, die Lose kaufen.
Die Zufallsgröße \(X\) ist nach \(B(100;0{,}15)\) binomialverteilt.
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
2. Annahme- und Ablehnungsbereich der Nullhypothese vorformulieren
Der Annahme- und Ablehnungsbereich der Nullhypothese lässt sich durch die Vergabe zunächst noch unbekannter Grenzen \(k\) und \(k + 1\) vorformulieren. Zusammen bilden beide Bereiche alle Werte \(x_{i} \in \{0,1, \dots, 100\}\) ab, welche die Zufallsgröße \(X\) annehmen kann.
Die Nullhypothese „Mindestens 15 % der angesprochenen Besucher kaufen Lose" \((H_{0} \colon p \geq 0{,}15)\) wird abgelehnt, wenn unter den 100 angesprochenen Besuchern tendenziell wenige Besucher Lose kaufen.
\[ \textcolor{#cc071e}{\overline{A} = \{0, 1, \dots, k\}} \qquad A = \{k + 1, \dots, 100\}\]
3. Bedingung für den Signifikanztest aufstellen
Bedingung: Die Wahrscheinlichkeit für den Fehler 1. Art darf höchstens so groß sein wie das vorgegebene Signifikanzniveau \(\textcolor{#0087c1}{\alpha}\).
Einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\)
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\alpha\) überprüft eine Vermutung, dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Dabei darf die Wahrscheinlichkeit für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreichen.
Linksseitiger Signifikanztest
\[H_0 \colon p_0 \geq p \quad H_1 \colon p_1 < p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{0; 1; ...; k\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
Rechtsseitiger Signifikanztest
\[H_0 \colon p_0 \leq p \quad H_1 \colon p_1 > p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{k + 1; ...; n\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 &&| \textcolor{red}{\cdot (-1)} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
ST: Stochastisches Tafelwerk
„... auf dem Signifikanzniveau von 10 %."
\(\Longrightarrow \quad \textcolor{#0087c1}{\alpha = 0{,}1}\)
Fehler 1. Art: Die Nullhypothese trifft zu, wird aber irrtümlich abgelehnt.
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\[\begin{align*}P(\text{Fehler 1. Art}) & \; \textcolor{#0087c1}{\leq \alpha} \\[0.8em] P_{\textcolor{#e9b509}{p_{0}}}^{n}(X \in \textcolor{#cc071e}{\overline{A}}) & \; \textcolor{#0087c1}{\leq \alpha} & &| \; \textcolor{#cc071e}{\overline{A} = \{0, 1, \dots, k\}} \\[0.8em] P_{\textcolor{#e9b509}{0{,}15}}^{100}(X \textcolor{#cc071e}{\leq k}) & \; \textcolor{#0087c1}{\leq 0{,}1} \end{align*}\]
(vgl. Anmerkung 1)
4. Entscheidungsregel formulieren
Mithilfe des Stochastischen Tafelwerks (ST) lassen sich die Grenzen \(k\) und \(k + 1\) des Ablehnungs- bzw. Annahmebereich der Nullhypothese ermitteln.
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Für den Parameter \(p = 0{,}15\) sucht man in der rechten Spalte (kumulative Verteilungsfunktion) der Tabelle \(n = 100\) denjenigen Wert \(P_{0{,}15}^{100}(X \leq k) = \sum \limits_{i\,=\,0}^{k}B(100;0{,}15;i)\), der höchstens \(0{,}1\) beträgt und notiert den zugehörigen Wert \(k\).
\[\overset{\text{ST}}{\Longrightarrow} \quad k = 10 \quad \left(P_{0{,}15}^{100}(X \leq 10) = \sum \limits_{i\,=\,0}^{10}B(100;0{,}15;i) \overset{\text{ST}}{=} 0{,}09945 \right)\]
Mit \(k = 10\) und \(k + 1 = 11\) kann der Annahme- und der Ablehnungsbereich der Nullhypothese konkretisiert werden.
\[\overline{A} = \{0, 1, \dots, 10\} \qquad A = \{11, 12, \dots, 100\}\]
(vgl. Anmerkung 3)
Wenn höchstens 10 von den angesprochenen Besuchern Lose kaufen, wird die Inhaberin dem Angestellten das Gehalt kürzen.
oder
Wenn mindestens 11 von den angesprochenen Besuchern Lose kaufen, wird die Inhaberin dem Angestellten das Gehalt nicht kürzen.
{zen-hand-o-right}Anmerkung 1:{/zen-hand-o-right}
Da der Ablehnungsbereich \(\overline{A} = \{0, 1, \dots, k\}\) „links" der Werte \(x_{i} \in \{0,1, \dots, 100\}\) liegt, welche die Zufallsgröße \(X\) annehmen kann, handelt es sich um einen linksseitigen Signifikanztest.
Für die Bearbeitung einer Aufgabe zum Thema Signifikanztest ist die Unterscheidung nach linksseitigem und rechtsseitigem Signifikanztest nicht zwingend erforderlich. Es sei denn, die Aufgabenstellung verlangt dies ausdrücklich. Entscheidend ist die Festlegung der Nullhypothese und des Ablehnungsbereichs der Nullhypothese. Wie die Nullhypothese lautet, ergibt sich aus der Aufgabenstellung. Die Art der Nullhypothese lässt auf den Ablehnungsbereich der Nullhypothese schließen.
{zen-hand-o-right}Anmerkung 2:{/zen-hand-o-right}
Bei einem Signifikanztest betrachtet man im Falle einer Nullhypothese \(H_{0} \colon p \leq p_{0}\) oder \(H_{0} \colon p \geq p_{0}\) den „Extremfall" \(p = p_{0}\), um den Annahme- und Ablehnungsbereich der Nullhypothese zu bestimmen. Damit ist gewährleistet, dass die Wahrscheinlichkeit für den Fehler 1. Art auch für \(p < p_{0}\) bzw. \(p > p_{0}\) nicht das Signifikanzniveau \(\alpha\) überschreitet.
Im Falle der Nullhypothese \(H_{0} \colon p \geq 0{,}15\) genügt es also, den „Extremfall" \(p_{0} = 0{,}15\) zu betrachten.
{zen-hand-o-right}Anmerkung 3:{/zen-hand-o-right}
Mit dem Ablehnungsbereich \(\overline{A} = \{0, 1, \dots, 10\}\) liegt die maximale Wahrscheinlichkeit für den Fehler 1. Art \(P_{0{,}15}^{100}(X \leq 10) \approx 0{,}09945\) unter dem vorgegebenen Signifikanzniveau \(\alpha = 0{,}1\).
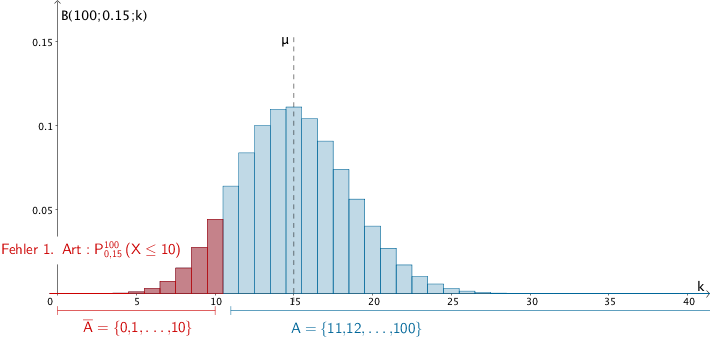
Linksseitiger Signifikanztest der Nullhypothese \(H_{0} \colon p \geq 0{,}15\) zum Signifikanzniveau \(\alpha = 10\,\%\) bei einem Stichprobenumfang von \(n = 100\) (verkürzte Darstellung bis \(k = 40\))


