Für jedes \(a \in \mathbb R^{+}\) liegt die Gerade \(g_{a}\) in der Ebene \(U\) mit der Gleichung \(x_{1} = 2{,}5\).
Ein beliebiger Punkt \(P(p_{1}|p_{2}|p_{3})\) des Raums wird an der Ebene \(U\) gespiegelt. Geben Sie die Koordinaten des Bildpunkts \(P'\) in Abhängigkeit von \(p_{1}\), \(p_{2}\) und \(p_{3}\) an.
(2 BE)
Lösung zu Teilaufgabe d
\(U \colon x_{1} = 2{,}5\), \(P(p_{1}|p_{2}|p_{3})\)
Koordinaten des Bildpunktes: \(P'(5 - p_{1}|p_{2}|p_{3})\)
Begründung (nicht verlangt):
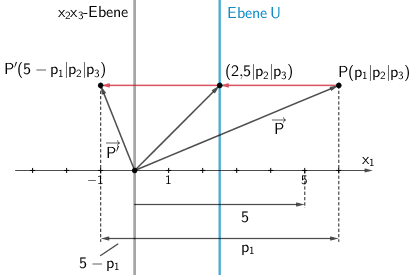
Da die Ebene \(U\) parallel zur \(x_{2}x_{3}\)-Ebene liegt, ändert sich bei der Spiegelung eines beliebigen Punktes \(P(p_{1}|p_{2}|p_{3})\) an der Ebenen \(U\) nur die \(x_{3}\)-Koordinate. Die Gerade \(PP'\) schneidet die Ebene \(U\) im Punkt \((2{,}5|p_{2}|p_{3})\).
Durch Vektoraddition ergibt sich:
\[\overrightarrow{P'} = \begin{pmatrix} 2{,}5 \\ p_{2} \\ p_{3} \end{pmatrix} + \textcolor{#cc071e}{\begin{pmatrix} 2{,}5 - p_{1} \\ p_{2} - p_{2} \\ p_{3} - p_{3} \end{pmatrix}} = \begin{pmatrix} 5 - p_{1} \\ p_{2} \\ p_{3} \end{pmatrix}\]
\[\Longrightarrow \quad P'(5 - p_{1}|p_{2}|p_{3})\]
oder
\[\begin{align*}\overrightarrow{P'} &= \overrightarrow{P} + \textcolor{#cc071e}{2 \cdot \begin{pmatrix} 2{,}5 - p_{1} \\ p_{2} - p_{2} \\ p_{3} - p_{3} \end{pmatrix}} \\[0.8em] &= \begin{pmatrix} p_{1} \\ p_{2} \\ p_{3} \end{pmatrix} + \begin{pmatrix} 5 - 2p_{1} \\ 0 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 5 - p_{1} \\ p_{2} \\ p_{3} \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad P'(5 - p_{1}|p_{2}|p_{3})\]


