Gegeben sind die Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\).
a) Weisen Sie nach, dass sich die Geraden \(g\) und \(h\) im Punkt \(S(-3|-1|4)\) schneiden.
b) Geben Sie eine Gleichung der von den Geraden \(g\) und \(h\) aufgespannten Ebene \(E\) in Parameterform an und bestimmen Sie ein Gleichung der Ebene \(E\) in Normalenform.
a) Nachweis, dass sich die Geraden \(g\) und \(h\) im Punkt \(S(-3|-1|4)\) schneiden
Für die Berechnung des Schnittpunkts \(S\) der Geraden \(g\) und \(h\) werden die Ortsvektoren \(\overrightarrow{X}_{g}\) und \(\overrightarrow{X}_{h}\) der Geradengleichungen von \(g\) und \(h\) gleichgesetzt (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden).
\[g \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
\[\begin{align*} \overrightarrow{X}_{g} &= \overrightarrow{X}_{h} \\[0.8em] \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} &= \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix} \end{align*}\]
Liest man die Vektorgleichung zeilenweise, ergibt sich ein (überbestimmtes) lineares Gleichungssystem mit drei Gleichungen und den beiden zu bestimmenden Unbekannten \(\lambda\) und \(\mu\).
\[\begin{align*} \text{I} & & -5 + 6\lambda &= -6 + 3\mu \\[0.8em] \text{II} & & \wedge -2 + 3\lambda &= -8 + 7\mu \\[0.8em] \text{III} & & \wedge \enspace \enspace \: 5 - 3\lambda &= \enspace \: 3 + \enspace \mu \end{align*}\]
Aus je zwei Gleichungen lassen sich die Werte von \(\lambda\) und \(\mu\) bestimmen. Die Lösung ist nur dann eindeutig, wenn die ermittelten Werte für \(\lambda\) und \(\mu\) die dritte Gleichung erfüllen (wahre Aussage).
In diesem Fall bietet es sich an, auf die Gleichungen II und III das Additionsverfahren anzuwenden, um in einem ersten Schritt den Wert des Parameters \(\mu\) zu ermitteln.
\[\begin{align*} \text{II} + \text{III} \colon -2 + 5 + 3\lambda - 3\lambda &= -8 + 3 + 7\mu + \mu \\[0.8em] 3 + 0 &= -5 + 8\mu &&| + 5 \\[0.8em] 8 &= 8\mu &&| : 8 \\[0.8em] 1 &= \mu \end{align*}\]
\[\begin{align*} \mu = 1 \; \text{in III}\colon 5 - 3\lambda &= 3 + 1 \\[0.8em] 5 - 3\lambda &= 4 &&| - 5 \\[0.8em] -3\lambda &= -1 &&| : (-3) \\[0.8em] \lambda &= \frac{1}{3} \end{align*}\]
\[\begin{align*} \lambda = \frac{1}{3}, \; \mu = 1 \; \text{in I}\colon -5 + 6 \cdot \frac{1}{3} &= 3 + 1 \\[0.8em] -5 + 2 &= -6 + 3 \\[0.8em] -3 &= -3 \quad(\text{w}) \end{align*}\]
Also ist \(\lambda = \frac{1}{3}\) und \(\mu = 1\) eine eindeutige Lösung des Gleichungssystems.
Um den Ortsvektor \(\overrightarrow{S}\) des Schnittpunkts \(S\) zu bestimmen, wird entweder \(\lambda = \frac{1}{3}\) in die Gleichung der Gerade \(g\) oder \(\mu = 1\) in die Gleichung der Geraden \(h\) eingesetzt.
\[S \in g \colon \overrightarrow{S} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \frac{1}{3} \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} = \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix} \quad \Longrightarrow \quad S(-3|-1|4)\]
\[S \in h \colon \overrightarrow{S} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + 1 \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix} = \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix} \quad \Longrightarrow \quad S(-3|-1|4)\]
b) Gleichung der von den Geraden \(g\) und \(h\) aufgespannten Ebene \(E\) in Parameterform sowie Bestimmung einer Gleichung der Ebene \(E\) in Normalenform
Gleichung der von den Geraden \(g\) und \(h\) aufgespannten Ebene \(E\) in Parameterform
\[g \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
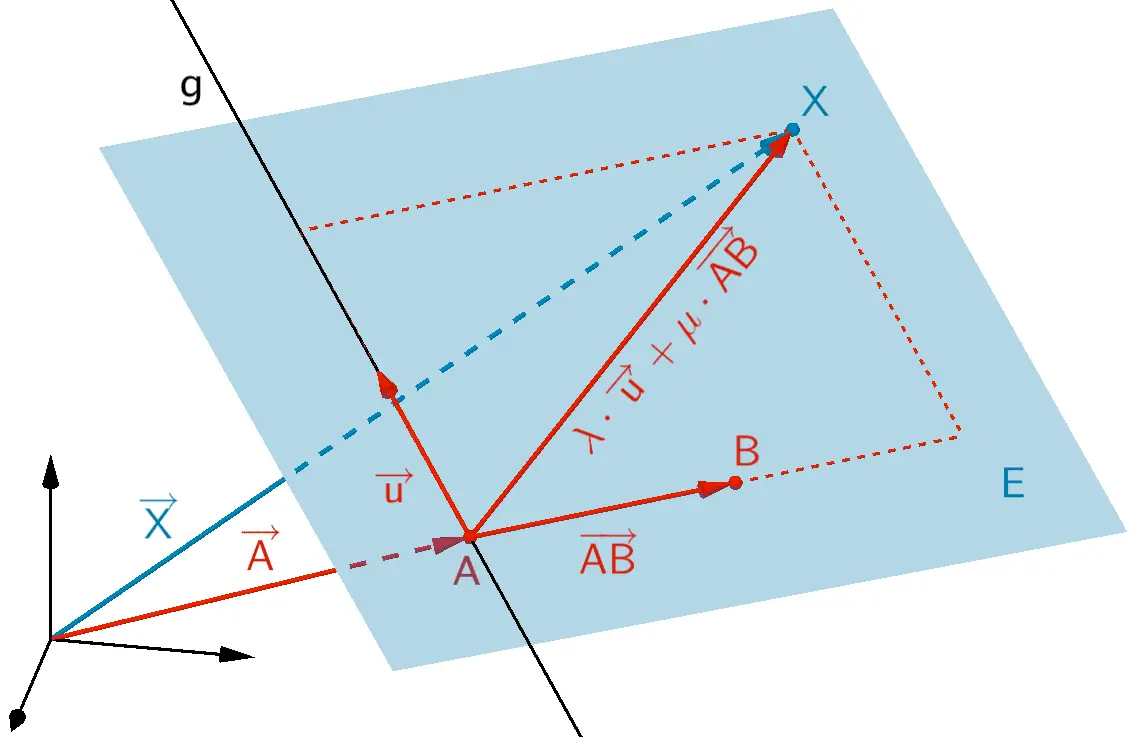
Veranschaulichung: Zwei sich schneidende Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\) legen die Gleichung einer Ebene \(E\) eindeutig fest. Beispiel: \(E \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} + \mu \cdot \overrightarrow{AB}; \; \lambda, \mu \in \mathbb R\) (vgl. Abiturskript - 2.2.2 Ebenengleichung in Parameterform)
Wählt man einen Stützvektor der Geradengleichung von \(g\) oder \(h\) und die beiden (linear unabhängigen) Richtungsvektoren der Geradengleichungen als Spannvektoren, so ergeben sich folgende mögliche Gleichungen der Ebene \(E\) in Parameterform:
\[E \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
oder
\[E \colon \overrightarrow{X} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \lambda, \mu \in \mathbb R\]
Bestimmung einer Gleichung der Ebene \(E\) in Normalenform
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
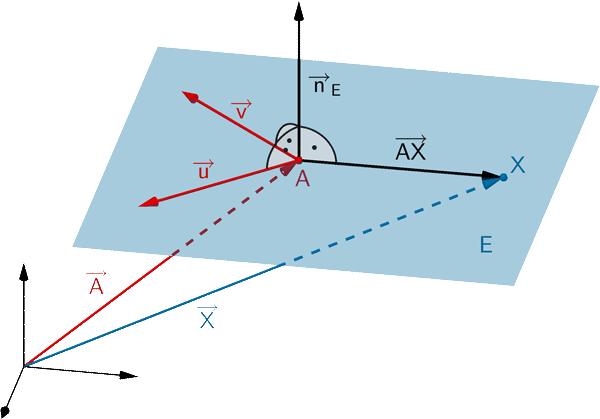
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
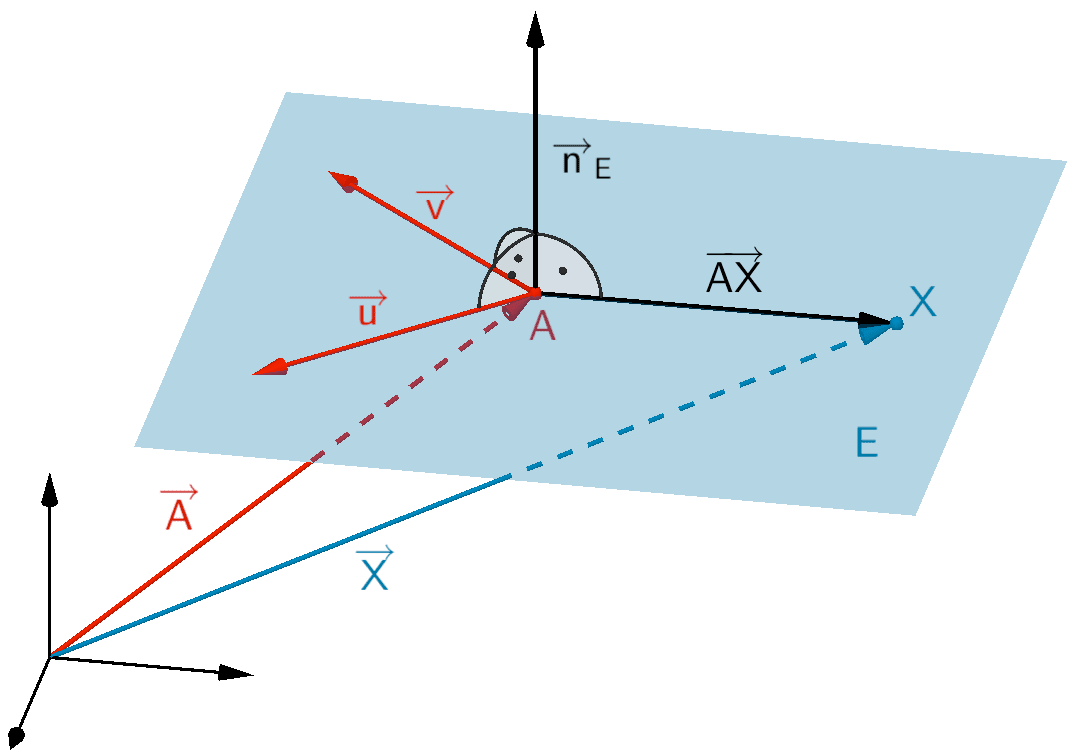
Veranschaulichung: Normalenform einer Ebene \(E\) (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform)
Das Vektorprodukt der beiden (linear unabhängigen) Richtungsvektoren der Geraden \(g\) und \(h\) liefert einen Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Der Ansatz für die Gleichung der Ebene \(E\) in Normalenform kann mit der Vektordarstellung oder der Koordinatendarstellung erfolgen.
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) bestimmen:
\[g \colon \overrightarrow{X} = \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -6 \\ -8 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \begin{pmatrix} 6 \\ 3 \\ -3 \end{pmatrix} \times \begin{pmatrix} 3 \\ 7 \\ 1 \end{pmatrix} &= \begin{pmatrix} 3 & \cdot & 1 & - & (-3) & \cdot & 7 \\ (-3) & \cdot & 3 & - & 6 & \cdot & 1 \\ 6 & \cdot & 7 & - & 3 & \cdot & 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 24 \\ -15 \\ 33 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 8 \\ -5 \\ 11 \end{pmatrix} \end{align*}\]
Also ist der Vektor \(\overrightarrow{n}_{E} = \begin{pmatrix} 8 \\ -5 \\ 11 \end{pmatrix}\) ein Normalenvektor der Ebene \(E\).
Die Aufgabenstellung verlangt nach der Gleichung der Ebene \(E\) in Normalenform. Ob in der Vektordarstellung oder in der Koordinatendarstellung ist frei wählbar.
1. Möglichkeit: Ansatz mit Vektordarstellung
Es wird beispielsweise der Stützvektor \(\begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix}\) der Geradengleichung von \(g\) als Stützvektor für die Gleichung der Ebene \(E\) verwendet. Damit lässt sich die Gleichung der Ebene \(E\) in Normalenform in der Vektordartsellung wie folgt angeben:
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon \begin{pmatrix} 8 \\ -5 \\ 11 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} \right] = 0\]
Durch Ausmultiplizieren des Skalarproduks erhält man die Ebenengleichung in Normalenform in der Koordinatendarstellung.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} 8 \\ -5 \\ 11 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix} \right] &= 0 \\[0.8em] 8 \cdot (x_{1} - (-5)) + (-5) \cdot (x_{2} - (-2)) + 11 \cdot (x_{3} - 5) &= 0 \\[0.8em] 8x_{1} + 40 - 5x_{2} - 10 + 11x_{3} - 55 &= 0 \\[0.8em] 8x_{1} - 5x_{2} + 11x_{3} - 25 &= 0 \end{align*}\]
\[\Longrightarrow \quad E \colon 8x_{1} - 5x_{2} + 11x_{3} - 25 = 0 \]
2. Möglichkeit: Ansatz mit Koordinatendarstellung
Beispielsweise entnimmt man dem Stützvektor \(\begin{pmatrix} -5 \\ -2 \\ 5 \end{pmatrix}\) der Geradengleichung von \(g\), dass der Punkt \((-5|-2|5)\) in der Ebene \(E\) liegt.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\(\overrightarrow{n}_{E} = \begin{pmatrix} 8 \\ -5 \\ 11 \end{pmatrix}; \; (-5|-2|5) \in E\)
\[\begin{align*} &E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0 \\[0.8em] &E \colon 8x_{1} - 5x_{2} + 11x_{3} + n_{0} = 0 \end{align*}\]
Mit \((-5|-2|5) \in E\) lässt sich \(n_{0}\) berechnen.
\[\begin{align*} (-5|-2|5) \in E \colon 8 \cdot (-5) - 5 \cdot (-2) + 11 \cdot 5 + n_{0} &= 0 \\[0.8em] -40 + 10 + 55 + n_{0} &= 0 \\[0.8em] 25 + n_{0} &= 0 &&| - 25 \\[0.8em] n_{0} &= -25 \end{align*}\]
\[\Longrightarrow \quad E \colon 8x_{1} - 5x_{2} + 11x_{3} - 25 = 0 \]

