Der Graph \(G_{f}\) einer gebrochenrationalen Funktion \(f\) hat folgende Eigenschaften:
\(G_{f}\) hat genau die zwei Nullstellen \(x = 0\) und \(x = 4\).
\(G_{f}\) hat genau die zwei Polstellen mit Vorzeichenwechsel \(x = -1\) und \(x = 2\).
\(G_{f}\) hat eine waagrechte Asymptote mit der Gleichung \(y = 2\).
a) Geben Sie einen möglichen Funktionsterm der Funktion \(f\) an und skizzieren Sie den Graphen der Funktion \(f\).
b) „Der Funktionsterm \(f(x)\) ist durch die genannten Eigenschaften eindeutig bestimmt." Nehmen Sie zu dieser Aussage begründend Stellung.
a) Möglicher Funktionsterm der Funktion \(f\) und Skizze des Graphen \(G_{f}\)
Möglicher Funktionsterm der Funktion \(f\)
Gesucht ist eine gebrochenrationale Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), welche die genannten Eigenschaften erfüllt. Die Eigenschaften lassen sich schrittweise berücksichtigen.
1. Eigenschaft „\(G_{f}\) hat genau die zwei Nullstellen \(x = 0\) und \(x = 4\)" berücksichtigen:
Das Zählerpolynom \(z(x)\) bestimmt die Nullstellen der gebrochenrationalen Funktion \(f\). In Kenntnis der Nullstellen \(x = 0\) und \(x = 4\) wird das Zählerpolynom \(z(x)\) zunächst als Produkt der Linearfaktoren \((x - 0)\) und \((x - 4)\) formuliert.
\[\Longrightarrow \quad z(x) = (x - 0)(x - 4) = x(x - 4) = x^{2} - 4x\]
2. Eigenschaft „\(G_{f}\) hat genau die zwei Polstellen mit Vorzeichenwechsel \(x = -1\) und \(x = 2\)" berücksichtigen:
An den Nullstellen des Nennerpolynoms \(n(x)\), die nicht zugleich Nullstellen des Zählerpolynoms \(z(x)\) sind, besitzt eine gebrochenrationale Funktion Polstellen. Im Falle ungerader Nennernullstellen sind dies Polstellen mit Vorzeichenwechsel (Polstellen ungerader Ordnung). In Kenntnis der Polstellen \(x = -1\) und \(x = 2\) wird das Nennerpolynom beispielsweise als Produkt der Linearfaktoren \((x + 1)\) und \((x -2)\) (einfache Nennernullstellen) angegeben.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\[\Longrightarrow \quad n(x) = (x + 1)(x - 2) = x^{2} - x - 2\]
3. Eigenschaft „\(G_{f}\) hat eine waagrechte Asymptote mit der Gleichung \(y = 2\)" berücksichtigen:
Sind das Zählerpolynom \(z(x)\) und das Nennerpolynom \(n(x)\) vom selben Grad, bestimmt eine waagrechte Asymptote, die nicht die \(x\)-Achse ist, das Verhalten des Graphen einer gebrochenrationalen Funktion im Unendlichen.
Die Gleichung der waagrechten Asymptote ergibt sich aus dem Quotienten der Koeffizienten der höchsten Potenzen des Zähler- und Nennerpolynoms. Mit den bereits gewählten Polynomen \(z(x) = 1x^{2} - 4x\) und \(n(x) = 1x^{2} - x - 2\) lautet die Gleichung der waagrechten Asymptote \(y = \frac{1}{1}\), also \(y = 1\).
Damit der Graph \(G_{f}\) der gesuchten gebrochenrationalen Funktion \(f\) die waagrechte Asymptote \(y = 2\) besitzt, muss das Zählerpolynom \(z(x)\) um den Faktor \(2\) korrigiert werden.
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\[\Longrightarrow \quad z(x) = 2x(x - 4) = 2x^{2} - 8x \]
Probe durch Grenzwertbetrachtung:
\[\begin{align*}\lim \limits_{x\,\to\,\pm\infty} \frac{z(x)}{n(x)} &= \lim \limits_{x\,\to\,\pm\infty} \frac{2x^{2} - 8x}{x^{2} - x - 2} \\[0.8em] &= \lim \limits_{x\,\to\,\pm\infty} \frac{\cancel{x^{2}} \cdot \left( 2 - \frac{8}{x} \right)}{\cancel{x^{2}} \cdot \left( 1 - \frac{1}{x} - \frac{2}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x\,\to\,\pm\infty} \frac{2 - \overbrace{\frac{8}{x}}^{\to\,0}}{1 - \underbrace{\frac{1}{x}}_{\to\,0} - \underbrace{\frac{2}{x^{2}}}_{\to\,0}} \\[0.8em] &= \frac{2}{1} \\[0.8em] &= 2 \end{align*}\]
\(\Longrightarrow \quad\) Waggrechte Asymptote mit der Gleichung \(y = 2\)
Möglichen Funktionsterm \(f(x)\) angeben:
\[f(x) = \frac{2x(x - 4)}{(x + 1)(x - 2)}; \; D_{f} = \mathbb R \backslash \{-1;2\}\]
oder
\[f(x) = \frac{2x^{2} - 8x}{x^{2} - x - 2}; \; D_{f} = \mathbb R \backslash \{-1;2\}\]
Skizze des Graphen \(G_{f}\)
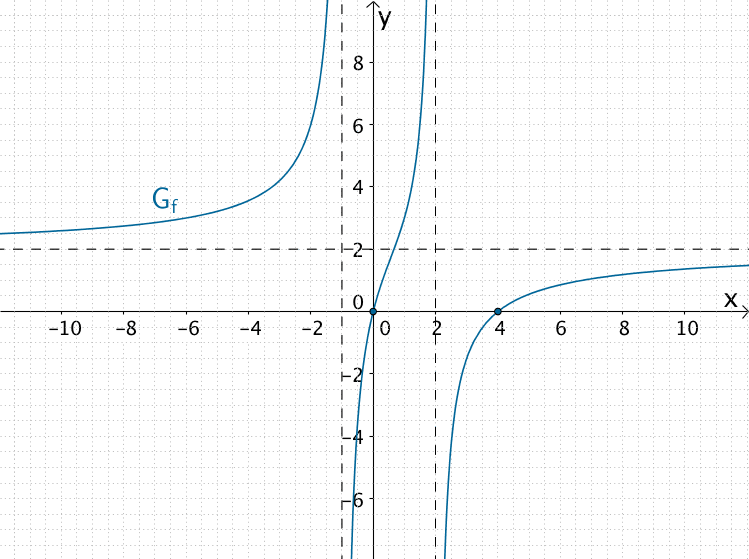
Verlauf des Graphen \(G_{f}\) der gebrochenrationalen \(Funktion f \colon x \mapsto \dfrac{2x(x - 4)}{(x + 1)(x - 2)}\) mit \(D_{f} = \mathbb R \backslash \{-1;2\}\)
b) Begründende Stellungnahme zu der Aussage: „Der Funktionsterm \(f(x)\) ist durch die genannten Eigenschaften eindeutig bestimmt."
Die Aussage ist falsch!
Begründung:
Die Eigenschaft „\(G_{f}\) hat genau die zwei Polstellen mit Vorzeichenwechsel \(x = -1\) und \(x = 2\)" legt den Funktionsterm der gesuchten gebrochenrationalen Funktion \(f\) nicht eindeutig fest.
Eine Polstelle mit Vorzeichenwechsel (Polstelle ungerader Ordnung) setzt eine Nennernullstelle ungerader Ordnung von \(f\) voraus. In der Lösung zu Teilaufgabe a wurden die einfachen Nennernullstellen \(x = -1\) und \(x = 2\) gewählt. Es sind beispielsweise auch dreifache Nennernullstellen denkbar, was bedeutet, dass die zugehörigen Linearfaktoren in dritter Potenz auftreten.
Unter Berücksichtigung aller genannter Eigenschaften der gesuchten gebrochenrationalen Funktion \(f\) könnte ein möglicher Funktionsterm beispielsweise auch wie folgt lauten:
\[f(x) = \frac{2x(x - 4)^{5}}{(x + 1)^{3}(x - 2)^{3}}; \; D_{f} = \mathbb R \backslash \{-1;2\}\]
oder
\[f(x) = \frac{2x^{5}(x - 4)}{(x + 1)^{3}(x - 2)^{3}}; \; D_{f} = \mathbb R \backslash \{-1;2\}\]
oder
\[f(x) = \frac{2x^{3}(x - 4)^{3}}{(x + 1)^{3}(x - 2)^{3}}; \; D_{f} = \mathbb R \backslash \{-1;2\}\]
usw.
Die zu berücksichtigenden Nullstellen \(x = 0\) und \(x = 4\) bleiben erhalten. Die Vielfachheit der Nullstellen ist so gewählt, dass der Grad des Zählerpolynoms weiterhin mit dem Grad des Nennerpolynoms übereinstimmt, um die waagrechte Asymptote mit der Gleichung \(y = 2\) zu gewährleisten.

