Betrachtet werden die folgenden Funktionsterme mit \(r,s \in \mathbb N\):
\(e(x) = \sqrt{x - r} \qquad \qquad \\ \)\(f(x) = \ln x \qquad \qquad \\ \)\(\displaystyle g(x) = -\frac{1}{x} + s\)
Jeder der Terme beschreibt genau einen der folgenden Funktionsgraphen I,II und III. Ordnen Sie die Terme den Graphen zu und geben Sie die Werte der Parameter \(r\) und \(s\) an; begründen Sie jeweils Ihre Antwort.
(5 BE)
Lösung zu Teilaufgabe 5
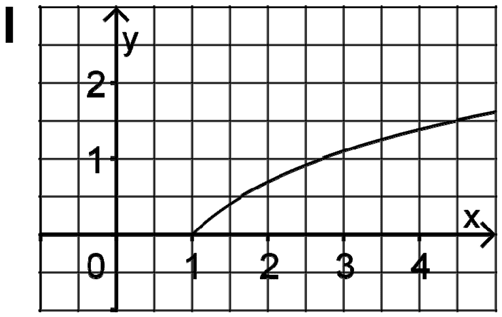
Graph I entspricht \(G_f\) der Funktion \(f(x) = \ln x\).
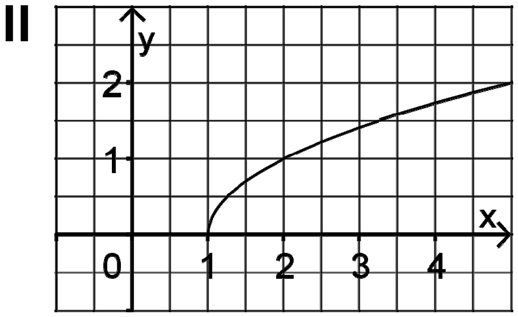
Graph II entspricht \(G_e\) der Funktion \(e(x) = \sqrt{x - r}\) mit \(r = 1\).
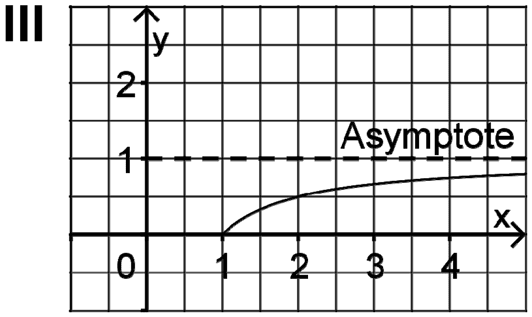
Graph III entspricht \(G_g\) der Funktion \(\displaystyle g(x) = -\frac{1}{x} + s\) mit \(s = 1\).
Zuordnung der Funktionsgraphen nach dem Ausschlussprinzip
1. Betrachtung von Graph III
Graph III zeigt die waagrechte Asymptote \(y = 1\). Von allen gegebenen Funktionen besitzt einzig die Funktion \(g(x) = -\frac{1}{x} + s\) eine waagrechte Asymptote.
\[\lim \limits_{x \to +\infty} g(x) = \lim \limits_{x \to +\infty} -\underset{\to 0}{\frac{1}{x}} + s = s\]
\(\Longrightarrow \quad y = s\) ist waagrechte Asymptote. \(\quad \Longrightarrow \quad s = 1\)
\(\Longrightarrow \quad g(x) = \frac{1}{x} + s\) gehört zu Graph III
2. Betrachtung der Funktion \(f(x) = \ln x\)
Typischer Funktionswert der Funktion \(f\):
Für die Funktion \(f(x) = \ln x\) gilt \(f(e) = \ln e = 1\).
Graph I verläuft durch den Punkt \((e \approx 2{,}7|1)\).
Steigung der Tangenten an Graph I an der Nullstelle \(x = 1\):
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
An Graph I lässt sich an der Stelle \(x = 1\) mit hinreichender Genauigkeit die Tangente \(t\) anlegen, welche die Steigung \(m_t = 1\) hat.
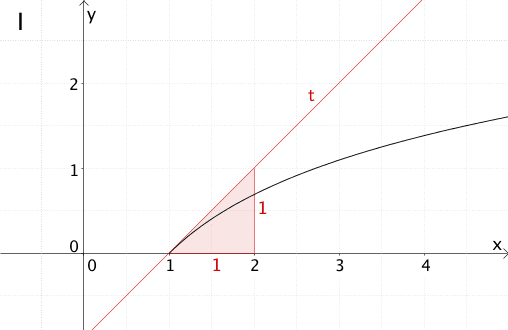
Tangente \(t\) an Graph I an der Stelle \(x = 1\)
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
(vgl. Merkhilfe)
\[f'(x) = \frac{1}{x}\]
\[f'(1) = \frac{1}{1} = 1 = m_t\]
\(\Longrightarrow \quad f(x) = \ln x\) gehört zu Graph I
3. Betrachtung von Graph ii)
Nach dem Ausschlussprinzip gehört die Funktion \(e(x) = \sqrt{x - r}\) zu Graph II. Dem Graphen entnimmt man den Punkt \((1|0)\).
\[\begin{align*} e(1) &= 0 \\[0.8em] \sqrt{1 - r} &= 0 & &| \; (\dots)^2 \\[0.8em] 1 - r &= 0 & &| +r \\[0.8em] 1 &= r \end{align*}\]
Steigung der Tangenten an Graph II an der Nullstelle \(x = 1\):
Zur Bestätigung, dass die Funktion \(e(x) = \sqrt{x - r}\) zu Graph II gehört, kann die Steigung der Tangente an Graph II an der Stelle \(x = 1\) betrachtet werden.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Graph II lässt vermuten, dass die Steigung \(m_t\) der Tangente \(t\) an der Stelle \(x = 1\) unendlich ist, da Graph II an der Stelle \(x = 1\) offensichtlich senkrecht auf der \(x\)-Achse steht.
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*} e(x) = \sqrt{x - 1} = (x - 1)^{\frac{1}{2}} \quad \Longrightarrow \quad e'(x) &= \frac{1}{2} \cdot (x - 1)^{-\frac{1}{2}} \\[0.8em] &= \frac{1}{2\sqrt{x - 1}} \end{align*}\]
Grenzwertbetrachtung von \(e'\) für \(x \to 1^+\):
\[\lim \limits_{x\,\to\,1^+} e'(x) = \lim \limits_{x\,\to\,1^+} \frac{1}{\underbrace{2\sqrt{x - 1}}_{\to\,0^+}} = +\infty \]
\[\Longrightarrow \quad m_t \to +\infty\]
\(\Longrightarrow \quad G_e \perp x\text{-Achse}\) an der Stelle \(x = 1\)
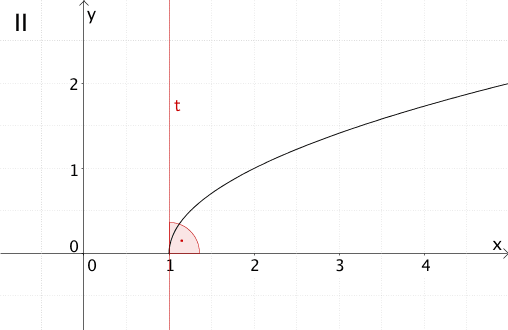
Die Steigung \(m_t\) der Tangente \(t\) an Graph II ist unendlich. Graph II ist an der Stelle \(x = 1\) senkrecht zur \(x-Achse\).


