Im Intervall \(]0;2[\) gibt es eine Stelle \(x_0\), an der der Wert der Differenz \(d(x) = q(x) - p(x)\) maximal wird. Berechnen Sie \(x_0\) sowie den Wert der zugehörigen Differenz.
(5 BE)
Lösung zu Teilaufgabe 1d
\[p(x) = -1{,}25x^2 + 5\,; \quad D_p = \mathbb R\]
\[q(x) = -0{,}11x^4 - 0{,}81x^2 + 5 \,; \quad D_q = \mathbb R\]
Differenzfunktion bilden:
\[\begin{align*}d(x) &= g(x) - p(x) \\[0.8em] &= -0{,}11x^4 - 0{,}81x^2 + 5 - \big( -1{,}25x^2 + 5 \big) \\[0.8em] &= -0{,}11x^4 + 0{,}44x^2 \end{align*}\]
Notwendige Bedingung für maximale Differenz: \(\,d^{\,\prime}(x) \overset{!}{=} 0\)
Erste Ableitung \(d^{\,\prime}(x)\) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*}d(x) = -0{,}11x^4 +0{,}44x^2 \quad \Longrightarrow \quad d^{\,\prime}(x) &= -0{,}11 \cdot 4x^3 + 0{,}44 \cdot 2x \\[0.8em] &= -0{,}44x^3 + 0{,}88x \\[0.8em] &= -0{,}44x\big(x^2 - 2\big)\end{align*}\]
\(x_0\) berechnen:
\[-0{,}44x\big(x^2 - 2\big) = 0\,; \quad x \in \; ]0;2[\]
\[\begin{align*}\Longrightarrow \quad x^2 - 2 &= 0 & &| +2 \\[0.8em] x^2 &= 2 & &| \; \sqrt{\quad} \\[0.8em] x_0 &= \sqrt{2}\end{align*}\]
Art der Exxtremstelle untersuchen:
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(d^{\,\prime\prime}(x)\) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*}d^{\,\prime}(x) = -0{,}44^3 + 0{,}88x \quad \Longrightarrow \quad d^{\,\prime\prime}(x) &= 3 \cdot (-0{,}44) \cdot x^2 + 0{,}88 \\[0.8em] &= -1{,}32x^2 + 0{,}88 \end{align*}\]
\[\begin{align*}d^{\,\prime\prime}(\sqrt{2}) &= -1{,}32 \cdot (\sqrt{2})^2 + 0{,}88 \\[0.8em] &= -1{,}32 \cdot 2 + 0{,}88 \\[0.8em] &= -1{,}76\end{align*}\]
\(\left. \begin{align*} d^{\,\prime}(\sqrt{2}) &= 0 \\[0.8em] d^{\,\prime\prime}(\sqrt{2}) &< 0 \end{align*} \right\} \Longrightarrow \quad\) Die Differenz \(d\) ist an der Stelle \(x_0 = \sqrt{2}\) maximal.
Wert der maximalen Differenz berechnen:
\[\begin{align*} d(\sqrt{2}) & = -0{,}11 \cdot (\sqrt{2})^4 + 0{,}44 \cdot (\sqrt{2})^2 \\[0.8em] &= -0{,}11 \cdot 4 + 0{,}44 \cdot 2 \\[0.8em] &= 0{,}44\end{align*}\]
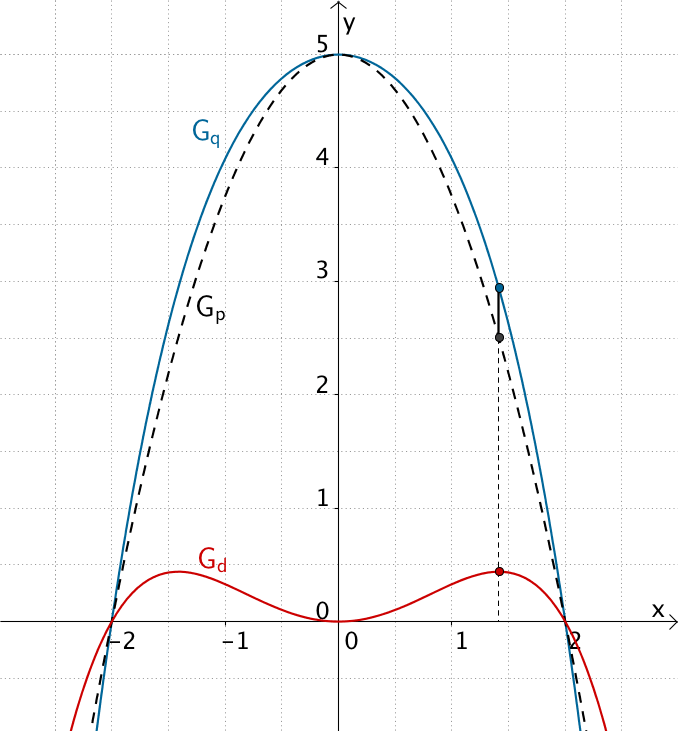
An der Stelle \(\,x_0 = \sqrt{2}\,\) ist der Wert der Differenz \(\,d(x) = q(x) - p(x)\,\) maximal.


