Der Graph der Funktion \(h\) ist streng monoton fallend und rechtsgekrümmt.
(2 BE)
Lösung zu Teilaufgabe 2b
Monoptoniekriterium, Krümmungsverhalten, Entwicklung von Funktionen
1. Lösungsansatz: Monotoniekriterium, Krümmungsverhalten
Für die gesuchte Funktion \(h\) muss im gesamten Definitionsbereich \(D_{h}\) gelten:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Der Graph der Funktion \(h\) ist streng monoton fallend.
\(\Longrightarrow \quad h'(x) < 0\)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Der Graph der Funktion \(h\) ist rechtsgekrümmt.
\(\Longrightarrow \quad h'' < 0\)
Diese Bedingungen erfüllt beispielsweise die in \(\mathbb R\) definierte Funktion \(h \colon x \mapsto -e^{x}\), denn es gilt:
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
(vgl. Merkhilfe)
\[h(x) = -e^{x}; \; D_{h} = \mathbb R\]
\[h'(x) = -e^{x} \quad \Longrightarrow \quad h'(x) < 0\]
\[h''(x) = -e^{x} \quad \Longrightarrow \quad h''(x) < 0\]
2. Lösungsansatz: Betrachtung der Natürliche Exponentialfunktion
Der Graph der natürlichen Exponetialfunktion \(f \colon x \mapsto e^{x}\) ist streng monoton steigend und in \(D_{f} = \mathbb R\) linksgekrümmt. Spiegelt man den Graphen der natürlichen Exponentialfunktion an der \(x\)-Achse, so ist der Graph der entstehenden Funktion \(h\) streng monoton fallend und in \(D_{h} = \mathbb R\) rechtsgekrümmt.
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[f(x) = e^{x}\; \; D_{f} = \mathbb R\]
\[h(x) = - f(x) = -e^{x}\]
\[\Longrightarrow \quad h(x) = -e^{x}; \; D_{h} = \mathbb R\]
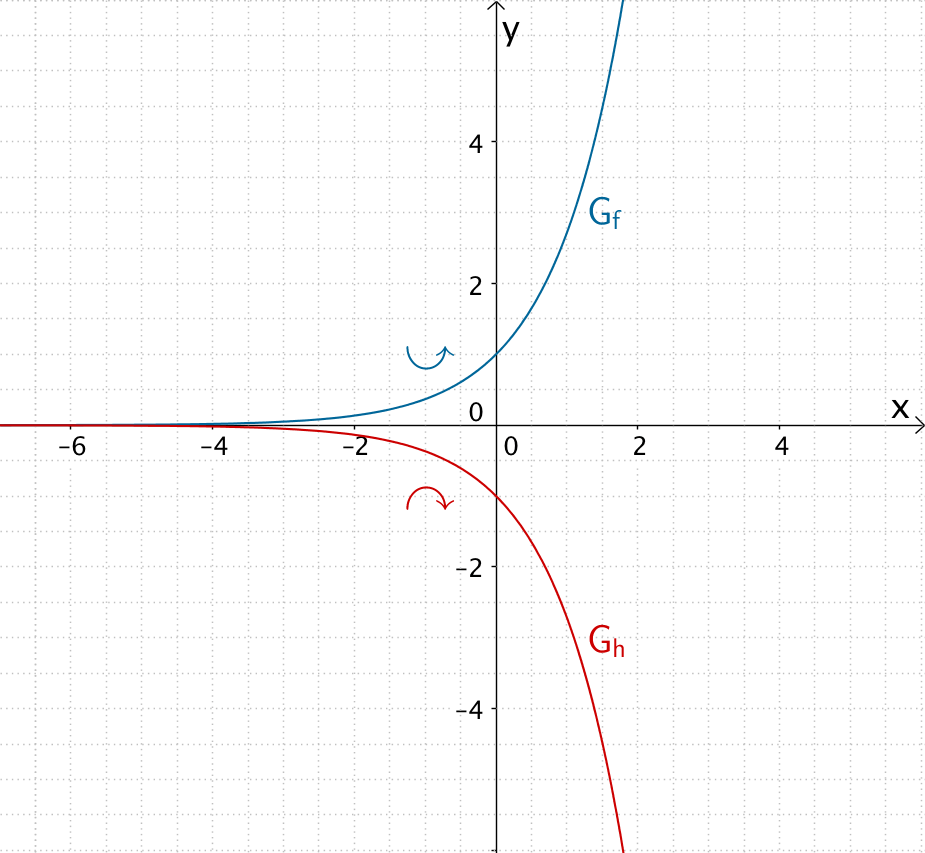
Streng monoton steigender, linksgekrümmter Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto e^{x}\) und streng monoton fallender, rechtsgekrümmter Graph der ebenfalls in \(\mathbb R\) definierten Funktion \(h \colon x \mapsto -e^{x}\)
3. Lösungsansatz: Betrachtung der Natürliche Logarithmusfunktion
Der Graph der natürlichen Logarithmusfunktion \(f \colon x \mapsto \ln{x}\) ist streng monoton steigend und in \(D_{f} = \mathbb R^{+}\) rechtsgekrümmt. Spiegelt man den Graphen der natürlichen Logarithmusfunktion an der \(y\)-Achse, so ist der Graph der entstehenden Funktion \(h\) streng monoton fallend und in \(D_{h} = \mathbb R^{-}\) rechtsgekrümmt.
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[f(x) = \ln{x}\; \; D_{f} = \mathbb R^{+}\]
\[h(x) = f(-x) = \ln(-x)\]
\[\Longrightarrow \quad h(x) = \ln(-x); \; D_{h} = \mathbb R^{-}\]
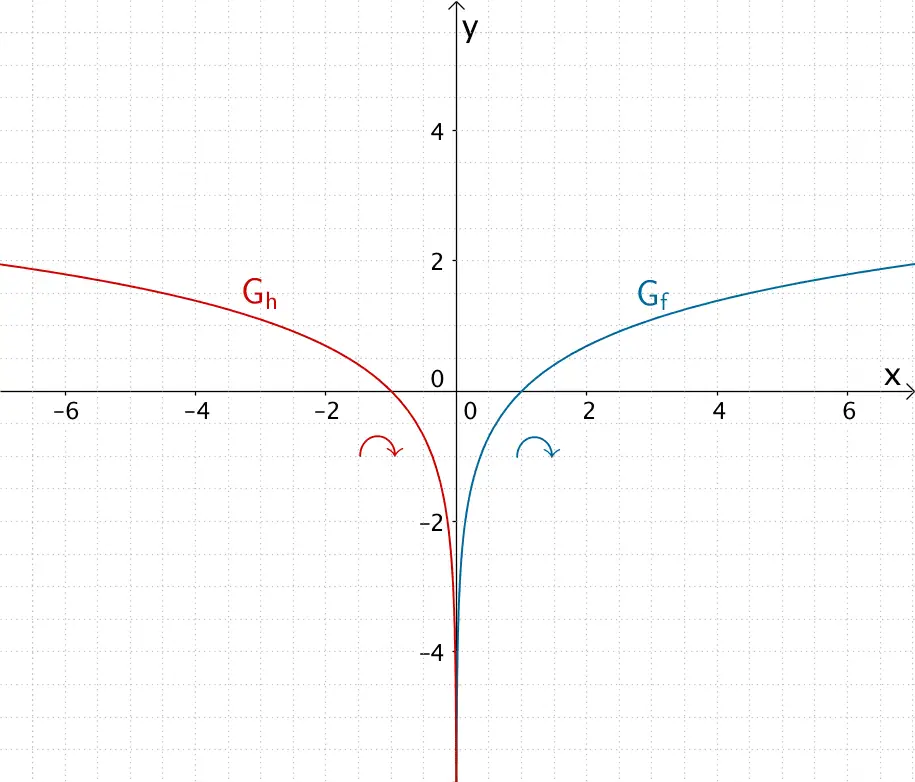
Streng monoton steigender, rechtsgekrümmter Graph der in \(\mathbb R^{+}\) definierten Funktion \(f \colon x \mapsto \ln{x}\) und streng monoton fallender, rechtsgekrümmter Graph der in \(\mathbb R^{-}\) definierten Funktion \(h \colon x \mapsto \ln(-x)\)


