Bestimmen Sie Lage und Art des Extrempunkts von \(G_{f}\).
(3 BE)
Lösung zu Teilaufgabe 1d
Extrempunkt bestimmen
\[f(x) = e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}; \; D = \mathbb R\]
Lage des Extrempunkts von \(G_{f}\)
Notwendige Bedingung für eine Extremstelle von \(G_{f}\):
\[f'(x) \overset{!}{=} 0\]
Aus Teilaufgabe 1c ist bekannt:
\[f'(x) = \frac{1}{2} \cdot \left( e^{\frac{1}{2}x} - e^{-\frac{1}{2}x} \right)\]
Nullstelle von \(f'\) bestimmen:
\[\begin{align*}f'(x) &= 0 \\[0.8em] \Longrightarrow \quad e^{\frac{1}{2}x} - e^{-\frac{1}{2}x} &= 0 & &| +e^{-\frac{1}{2}x} \\[0.8em] e^{\frac{1}{2}x} &= e^{-\frac{1}{2}x} & &| \; \ln \enspace \text{(Logarithmieren)} \\[0.8em] \ln\left( e^{\frac{1}{2}x} \right) &= \ln \left( e^{-\frac{1}{2}x} \right) & &| \; \log_{a}\left( a^{x} \right) = x \\[0.8em] \frac{1}{2}x &= -\frac{1}{2}x & &| + \frac{1}{2}x \\[0.8em] x &= 0 \end{align*}\]
Aus Teilaufgabe 1a ist bekannt: \(f(0) = 2\).
\(\Longrightarrow \quad\)Der Punkt \((0|2)\) ist einziger Extrempunkt von \(G_{f}\).
Art des Extrempunkts von \(G_{f}\)
1. Möglichkeit: Art von Extrempunkten mithilfe der zweiten Ableitung
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Aus Teilaufgabe 1c ist bekannt:
\(f''(x) > 0\) für \(x \in \mathbb R\)
\[\Longrightarrow \quad f''(0) > 0\]
\[\left. \begin{align*} &f'(0) = 0 \\[0.8em] &f''(0) > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt} \; TiP(0|2)\]
Alternative Argumentation in Zusammenhang mit der zweiten Ableitung \(f''\):
Aus Teilaufgabe 1c ist bekannt, dass \(G_{f}\) in \(\mathbb R\) linksgekrümmt ist. Folglich ist der Extrempunkt \((0|2)\) von \(G_{f}\) ein Tiefpunkt.
2. Möglichkeit: Monotoniekriterium bzw. Monotonietabelle
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[f'(x) = \frac{1}{2} \cdot \left( e^{\frac{1}{2}x} - e^{-\frac{1}{2}x} \right)\]
Um den Vorzeichenwechsel von \(f'(x)\) in der Umgebung der Extremstelle \(x = 0\) beurteilen und dokumentieren zu können, ist eine Skizze der Graphen der Funktionen \(x \mapsto e^{\frac{1}{2}x}\) und \(x \mapsto e^{-\frac{1}{2}x}\) hilfreich.
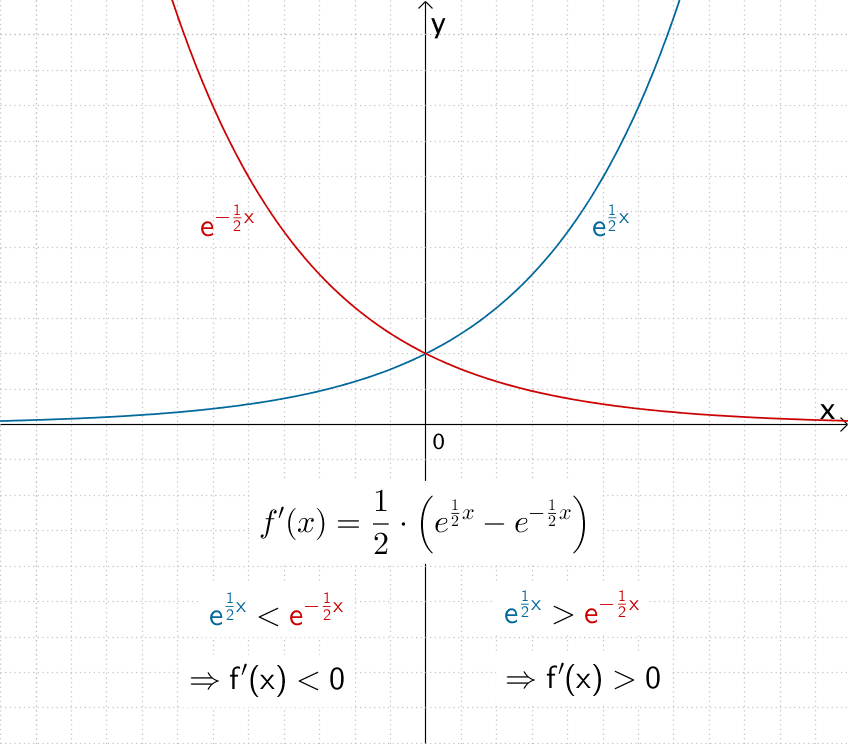
Vorzeichenwechsels von \(f'\) in der Umgebung der Extremstelle \(x = 0\) anhand einer Skizze der Graphen der Funktionen \(x \mapsto e^{\frac{1}{2}x}\) und \(x \mapsto e^{-\frac{1}{2}x}\)
\[\left. \begin{align*} &f'(x) < 0 \enspace \text{für} \enspace x < 0 \\[0.8em] &f'(0) = 0 \\[0.8em] &f'(x) > 0 \enspace \text{für} \enspace x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt} \; TiP(0|2)\]
Veranschaulichung mithilfe einer Monotonietabelle:
| \(x\) | \(x < 0\) | \(x = 0\) | \(x > 0\) |
| f'(x) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP\) | \(\nearrow\) |


