Gemäß der Kettenregel gilt \(g'(x) = f'\left( f(x) \right) \cdot f'(x)\). Ermitteln Sie damit und mithilfe von Abbildung 2 alle Stellen, an denen der Graph von \(g\) eine waagrechte Tangente besitzt.
(3 BE)
Lösung zu Teilaufgabe 3b
\[g'(x) = f'\left( f(x) \right) \cdot f'(x)\]
Die Bedingung dafür, dass der Graph von \(g\) eine waagrechte Tangente (Steigung gleich null) besitzt, lautet:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\textcolor{#cc071e}{g'(x) = 0}\]
Mit \(g'(x) = f'\left( f(x) \right) \cdot f'(x)\) ist die Bedingung erfüllt, falls \(\textcolor{#cc071e}{f'\left( f(x) \right) = 0}\) oder \(\textcolor{#cc071e}{f'(x) = 0}\).
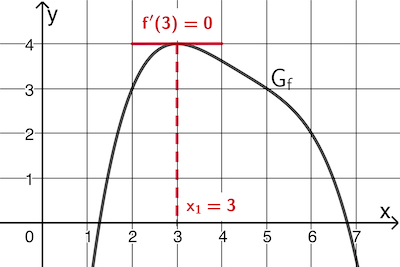 Abb. 2
Abb. 2
An der Stelle \(\textcolor{#cc071e}{x_1 = 3}\) besitzt \(G_f\) eine waagrechte Tangente und es gilt somit \(\textcolor{#cc071e}{f'(3) = 0}\) (vgl. Angabe Aufgabe 3).
Mit \(\textcolor{#cc071e}{f'(3) = 0}\) gilt \(\textcolor{#cc071e}{f'\left( \textcolor{#0087c1}{f(x)} \right) = 0}\), falls \(\textcolor{#0087c1}{f(x) = 3}\).
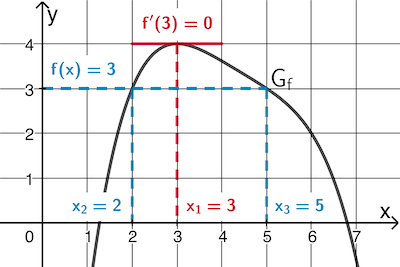 Abb. 2
Abb. 2
Mithilfe von Abbildung 2 gilt \(\textcolor{#0087c1}{f(x) = 3}\) für \(\textcolor{#0087c1}{x_2 = 2}\) und \(\textcolor{#0087c1}{x_3 = 5}\).
Somit besitz der Graph von \(g\) an den Stellen \(x = 2\), \(x = 3\) und \(x = 5\) jeweils eine waagrechte Tangente.

