Im Rahmen eines Screenings wird eine sehr große Anzahl zufällig ausgewählter neugeborener Kinder getestet. Ermitteln Sie die pro Million getesteter KInder im Mittel zu erwartende Anzahl derjenigen Kinder, bei denen die Stoffwechselstörung vorliegt und das Testergebnis negativ ist.
(3 BE)
Lösung zu Teilaufgabe 2c
\(S\colon\enspace\)„Die Stoffwechselstörung liegt vor."
\(T\colon\enspace\)„Das Testergebnis ist positiv."
Wahrscheinlichkeit \(P(S \cap \overline{T})\) berechnen:
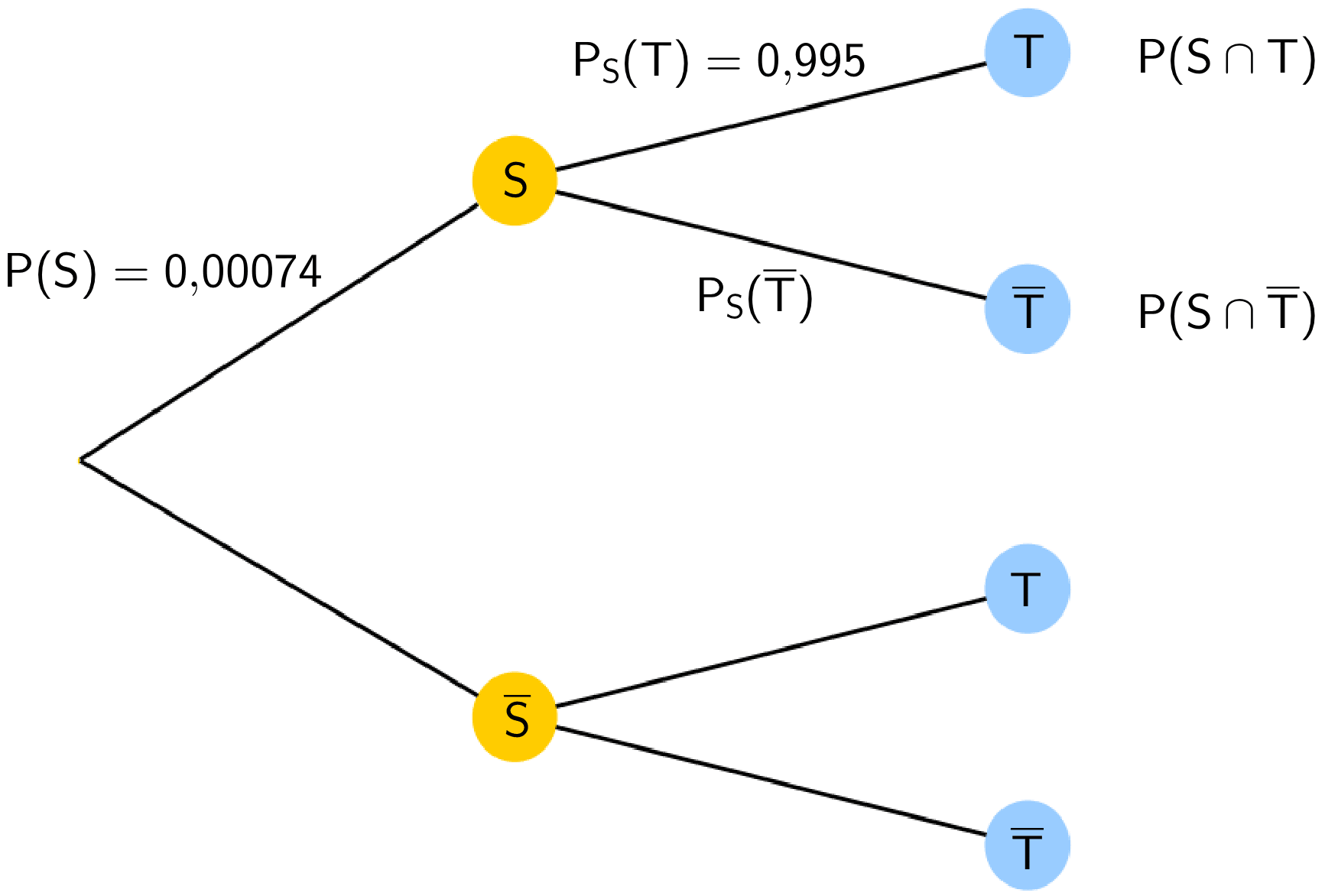
Baumdiagramm für die Ereignisse \(S\) und \(T\)
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Anwenden der Knotenregel:
\[\begin{align*}P_S(\overline{T}) &= 1 - P_S(T) \\[0.8em] &= 1 - 0{,}995 \\[0.8em] &= 0{,}005 \end{align*}\]
Anwenden der 1. Pfadregel:
\[\begin{align*}P(S \cap \overline{T}) &= P(S) \cdot P_S(\overline{T}) \\[0.8em] &= 0{,}00074 \cdot 0{,}005 \\[0.8em] &= 3{,}7 \cdot 10^{-6} \\[0.8em] &= \frac{3{,}7}{1\,\text{Mio}}\end{align*}\]
Das Ergebnis entspricht der relativen Häufigkeit \(h_{1\,\text{Mio}}\) bezogen auf eine Million getesteter Kinder \((n = 10^6 = 1\,\text{Mio})\).
Relative Häufigkeit eines Ereignisses \(\boldsymbol{E}\)
\[h_{n}(E) = \frac{H_{n}(E)}{n}\]
\(H_{n}(E)\): Anzahl mit der das Ereignis \(E\) entritt (absolute Häufigkeit)
\(n\): Anzahl der Durchführungen des Zufallsexperiments.
Absolute Häufigkeit \(H_{1\,\text{Mio}}\) berechnen:
\[h_{1\,\text{Mio}} = \frac{H_{1\,\text{Mio}}}{1\,\text{Mio}} \quad \Longleftrightarrow \quad H_{1\,\text{Mio}} = h_{1\,\text{Mio}} \cdot 1\,\text{Mio}\]
\[H_{1\,\text{Mio}} = \frac{3{,}7}{1\,\text{Mio}} \cdot 1\,\text{Mio} = 3{,}7\]
Pro Million getesteter Kinder sind im Mittel 3,7 KInder zu erwarten, bei denen die Stoffwechselstörung vorliegt und das Testergebnis negativ ist.


