Bei starkem Regen verformt sich das Sonnensegel und hängt durch. Es bildet sich eine sogenannte Wassertasche aus Regenwasser, das nicht abfließen kann. Die Oberseite der Wassertasche verläuft horizontal und ist näherungsweise kreisförmig mit einem Durchmesser von 50 cm. An ihrer tiefsten Stelle ist die Wassertasche 5 cm tief. Vereinfachend wird die Wassertasche als Kugelsegment betrachtet (vgl. Abbildung 2).
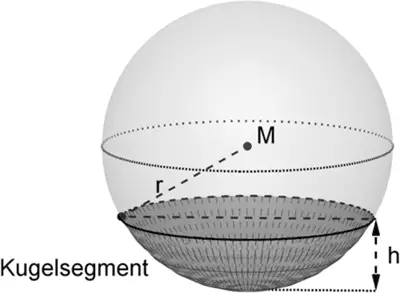 Abb. 2
Abb. 2
Das Volumen \(V\) eines Kugelsegments kann mit der Formel \(V = \frac{1}{3} \pi h^{2} \cdot (3r - h)\) berechnet werden, wobei \(r\) den Radius der Kugel und \(h\) die Höhe des Kugelsegments bezeichnen. Ermitteln Sie, wie viele Liter Wasser sich in der Wassertasche befinden.
(zur Kontrolle: \(r = 65\;\sf{cm}\))
(5 BE)
Lösung zu Teilaufgabe f
\[V = \frac{1}{3}\pi h^{2}\cdot (3r - h)\]
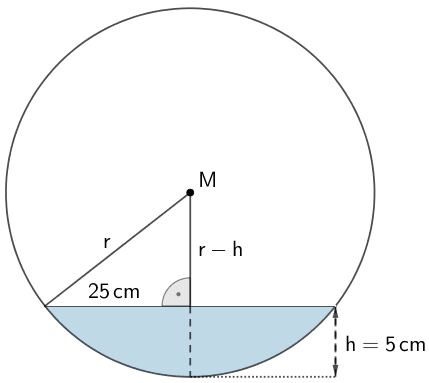
Der Radius \(r\) der Kugel lässt sich mithilfe des Satzes des Pythagoras berechnen.
Der Radius der kreisförmigen Oberseite der Wassertasche ist mit \(\frac{50\,\sf{cm}}{2} = 25\,\sf{cm}\) gegeben.
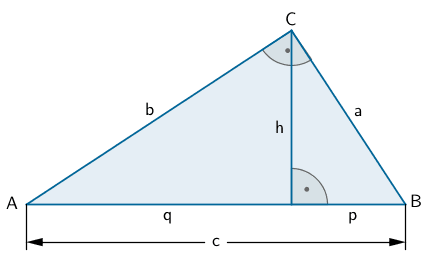
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} r^{2} &= 25^{2} + \underbrace{(r - 5)^{2}}_{\Large (a\,-\,b)^{2}} &&| \; \text{2. Binom. Formel anwenden} \\[0.8em] r^{2} &= 625 + \underbrace{r^{2} - 10r + 25}_{\Large a^{2}\,-\,2ab\,+\,b^{2}} &&| - r^{2} \\[0.8em] 0 &= 650 - 10r &&| + 10r \\[0.8em] 10 r &= 650 &&| : 10 \\[0.8em] r &= 65\end{align*}\]
Der Kugelradius \(r\) beträgt 65 cm.
Damit lässt sich das Volumen der Wassertasche wie folgt berechnen:
\[\begin{align*}V &= \frac{1}{3}\pi h^{2}\cdot (3r - h) \\[0.8em] &= \frac{1}{3}\pi \cdot 5^{2} \cdot (3 \cdot 65 - 5) \approx 4974\end{align*}\]
Das Volumen der Wassertasche beträgt ca. 4974 cm³.
Volumen in Liter:
Es gilt: 1000 cm³ = 1 l
\[V = \frac{4974}{1000} \approx 5\]
In der Wassertasche befinden sich ca. 5 Liter Regenwasser.


