Sonnenlicht, das an einem Sommertag zu einem bestimmten Zeitpunkt \(t_{0}\) auf die Sonnenuhr einfällt, wird im Modell durch parallele Geraden mit dem Richtungsvektor \(\overrightarrow{u} = \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\) dargestellt.
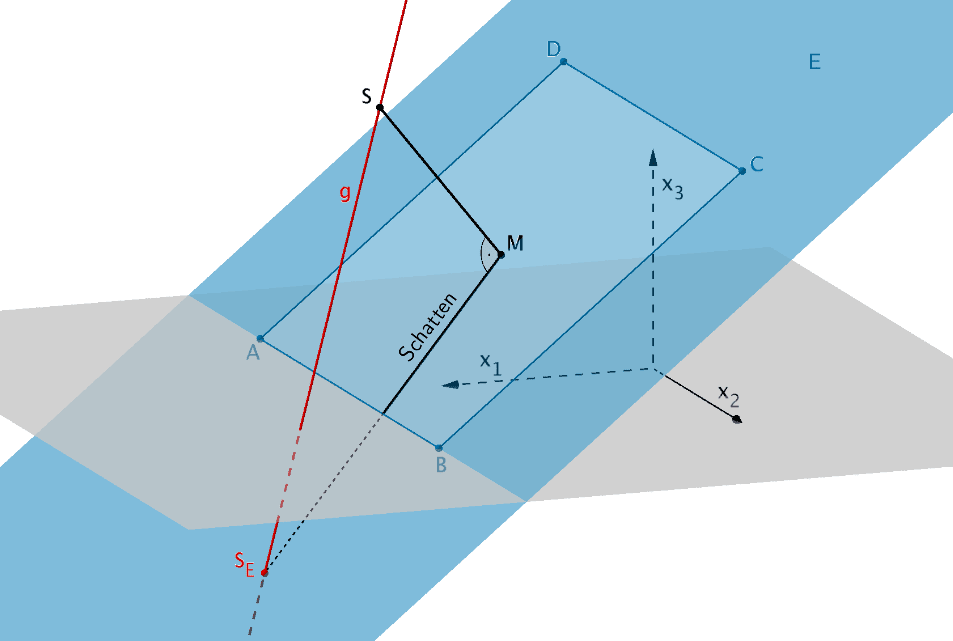
Weisen Sie nach, dass der Schatten der im Modell durch den Punkt \(S\) dargestellten Spitze des Polstabs außerhalb der rechteckigen Grundplatte liegt.
(6 BE)
Lösung zu Teilaufgabe d
Schnittpunkt Gerade - Ebene
\[\overrightarrow{u} = \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\]
Es sei \(g\) die Gerade, die im Modell den Anteil des Sonnenlichts darstellt, der zum Zeitpunkt \(t_{0}\) durch den Punkt \(S\) (Spitze des Polstabs) verläuft.
\[g\colon \overrightarrow{X} = \overrightarrow{S} + \lambda \cdot \overrightarrow{u}\,; \enspace \lambda \in \mathbb R\]
Anhand der Koordinaten des Vektors \(\overrightarrow{u}\) ist ersichtlich, dass die Sonne an besagtem Sommertag zum Zeitpunkt \(t_0\) bereits relativ hoch steht (negativer Wert der \(x_{3}\)-Koordinate). Es ist demnach zu erwarten, dass der Schatten des Polstabs die Kante \([AB]\) der Grundplatte erreicht.
Da die Grundplatte in der Ebene \(E\) liegt, markiert der Schnittpunkt \(S_{E}\) der Geraden \(g\) und der Ebene \(E\) den (fiktiven) Schatten der im Modell durch den Punkt \(S\) dargestellten Spitze des Polstabs. Folglich kann die Lage des Schnittpunkts \(S_{E}\) darüber Auskunft geben, dass die Spitze des Polstabs außerhalb der rechteckigen Grundplatte liegt.
Die Kante \([AB]\) verläuft mit \(A\,(5|-4|0)\) und \(B\,(5|4|0)\) im Modell in der \(x_{1}x_{2}\)-Ebene (\(x_{3} = 0\)). Die Spitze des Polstabs liegt somit dann außerhalb der Grundplatte, wenn für die \(x_{3}\)-Koordinate des Schnittpunkts \(S_{E}\) gilt: \(x_{3} < 0\).
Anmerkung: Lässt man die obige Überlegung zum Stand der Sonne anhand des Vektors \(\overrightarrow{u}\) außer acht und schließt die Möglichkeiten mit ein, dass der Schatten die Kante \([AD]\) oder \([BC]\) erreicht, so kann analog vorgegangen werden. Die Spitze des Polstabs liegt dann außerhalb der Grundplatte, wenn für die \(x_{2}\)-Koordiante des Schnittpunkts \(S_{E}\) entweder \(x_{2} < - 4\) (außerhalb der Kante \([AD]\) der Grundplatte) oder \(x_{2} > 4\) (außerhalb der Kante \([BC]\) der Grundplatte) gilt.
Schnittpunkt \(S_{E}\) der Geraden \(g\) mit der Ebene \(E\), Schatten des Polstabs auf der Grundplatte (Rechteck \(ABCD\))
Gleichung der Geraden \(g\) aufstellen:
\[S\,(4{,}5|0|4{,}5)\,, \enspace \overrightarrow{u} = \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\]
\[\begin{align*} &g\colon \overrightarrow{X} = \overrightarrow{S} + \lambda \cdot \overrightarrow{u} \\[0.8em] &g\colon \overrightarrow{X} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\end{align*}\]
Schnittpunkt \(S_{E}\) der Geraden \(g\) und der Ebene \(E\) bestimmen:
\[g\colon \overrightarrow{X} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\]
\[E\colon 4x_{1} + 5x_{3} - 20 = 0\]
Um den Schnittpunkt \(S_{E}\) der Geraden \(g\) und der Ebene \(E\) zu bestimmen, setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Ebenengleichung der Ebene \(E\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[\begin{align*}g \cap E\colon 4 \cdot (4{,}5 + 6\lambda) + 5 \cdot (4{,}5 - 13\lambda) - 20 &= 0 \\[0.8em] 18 + 24\lambda + 22{,}5 - 65\lambda - 20 &= 0 \\[0.8em] -41\lambda + 20{,}5 &= 0 & &| + 41\lambda \\[0.8em] 20{,}5 &= 41\lambda & &| : 41 \\[0.8em] \frac{1}{2} &= \lambda \end{align*}\]
Koordinaten des Schnittpunkts \(S_{E}\) berechnen:
Für die Besprechung der Koordinaten des Schnittpunkts \(S_{E}\) wird der Parameterwert von \(\lambda\) in die Geradengleichung von \(g\) eingesetzt.
\[\overrightarrow{S}_{E} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} + \frac{1}{2} \cdot \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} + \begin{pmatrix} 3 \\ 3 \\ -6{,}5 \end{pmatrix} = \begin{pmatrix} 7{,}5 \\ 3 \\ -2 \end{pmatrix}\]
\[\Longrightarrow \quad S_{E} (7{,}5|3|-2)\]
Da die \(x_3\)-Koordinate des Schnittpunkts \(S_{E}\) mit \(x_{3} = -2\) negativ ist, liegt der Schatten der Spitze des Polstabs außerhalb der rechteckigen Grundplatte.