Begründen Sie, dass \(G_{f}\) für \(x < 0\) nur im III. Quadranten verläuft, und zeichnen Sie in die Abbildung den darin fehlenden Teil von \(G_{f}\) ein. Berechnen Sie dazu \(f(-3)\) und drei weitere geeignete Funktionswerte von \(f\).

(4 BE)

Lösung zu Teilaufgabe c

Begründung, dass \(G_{f}\) für \(x < 0\) nur im III. Quadranten verläuft

\[f(x) = \frac{4x}{\underbrace{(x + 1)^{2}}_{>\,0}}; \; D_{f} = \mathbb R \backslash \{-1\}\]

Der Wert des Nenners von \(f\) ist in \(D_{f}\) stets positiv. Der Wert des Zählers ist für \(x < 0\) negativ. Somit ergeben sich für \(x < 0\) nur negative Funktionswerte von \(f\) und \(G_{f}\) verläuft folglich für \(x < 0\) nur im III. Quadranten. 

Berechnung von \(f(-3)\) und drei weiteren geeigneten Funktionswerten

Um den Verlauf von \(G_{f}\) für \(-1 < x < 0\) zu zeichnen, ist beispielsweise \(f(-0{,}25)\) ein geeigneter Funktionswert. Für die Zeichnung des Verlaufs von \(G_{f}\) für \(x < -1\) sind beispielsweise \(f(-4)\) und \(f(-6)\) zwei weitere geeignete Funktionswerte.

\[f(-0{,}25) = \frac{4 \cdot (-0{,}25)}{(-0{,}25 + 1)^{2}} \approx -1{,}8\]

\[f(-3) = \frac{4 \cdot (-3)}{(-3 + 1)^{2}}  = -3\]

\[f(-4) = \frac{4 \cdot (-4)}{(-4 + 1)^{2}}  \approx -1{,}8\]

\[f(-6) = \frac{4 \cdot (-6)}{(-6 + 1)^{2}}  \approx -0{,}96\]

Zeichnung von \(G_{f}\)

 

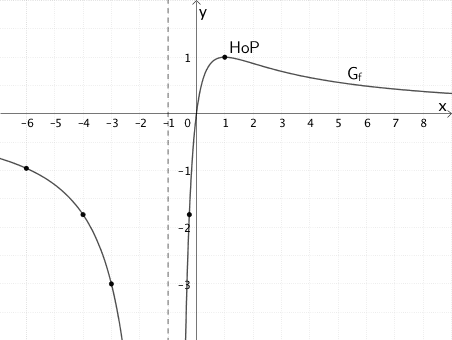
Verlauf des Graphen der Funktion \(f \colon x \mapsto \dfrac{4x}{(x + 1)^{2}}\) mit \(D_{f} = \mathbb R \backslash \{-1\}\)