Weisen Sie nach, dass die Wahrscheinlichkeit für einen Fehler zweiter Art bei diesem Ablehnungsbereich der Nullhypothese mehr als 50 % betragen könnte.
(4 BE)
Lösung zu Teilaufgabe 2c
Unter der Annahme, dass der Anteil der zufriedenen Abonnenten beispielsweise 65 % beträgt, trifft die Nullhypothese nicht zu.
Die Wahrscheinlichkeit für den Fehler 2. Art, dass die Nullhypothese nicht abgelehnt wird, obwohl sie nicht zutrifft, beträgt dann:
\[P_{0{,}65}^{200}(Y \leq 131) = 0{,}58520 \approx 58{,}5\,\% > 50\,\%\]
Ergänzende Erklärung (nicht verlangt)
Der Fehler 2. Art bedeutet: Die Nullhypothese wird nicht abgelehnt, obwohl sie nicht zutrifft.
In diesem Fall lautet die Nullhypothese \(H_0 \colon p \leq 0{,}6\) und die Gegenhypothese folglich \(H_1\colon p > 0{,}6\).
Annahmebereich \(\textcolor{#0087c1}{A = \{0;1;2; \dots\; 131\}}\) und Ablehnungsbereich \(\textcolor{#cc071e}{\overline{A} = \{132; 133; \dots;200\}}\) der Nullhypothese (vgl. Teilaufgabe 2b).
Die Wahrscheinlichkeit für einen Fehler 2. Art kann nur berechnet werden, wenn ein Wert für die Wahrscheinlichkeit der Gegenhypothese \(\textcolor{#e9b509}{p_1} > 0{,}6\) angenommen wird. Dann gilt:
\[P(\text{Fehler 2. Art}) = P_{\textcolor{#e9b509}{p_1}}^{n}(Y \in \textcolor{#0087c1}{A}) = P_{\textcolor{#e9b509}{p_1}}^{200}(Y \textcolor{#0087c1}{\leq 131})\]
Der angenommene Wert für \(\textcolor{#e9b509}{p_1}\) muss geeignet sein, um nachzuweisen, dass \(P_{\textcolor{#e9b509}{p_1}}^{200}(Y \textcolor{#0087c1}{\leq 131}) > 50\,\%\) sein kann. Wählt man hier willkürlich einen (im Tafelwerk tabellarisierten) Wert \(0{,}6 < \textcolor{#e9b509}{p_1} < 1\) stellt man fest, dass der Nachweis in den meisten Fällen nicht gelingt. Deshalb lohnt sich die Überlegung, ob \(\textcolor{#e9b509}{p_1}\) eher in der Nähe von \(p_0 = 0{,}6\) liegen sollte oder eher größer sein sollte.
Je größer der Wert von \(\textcolor{#e9b509}{p_1}\) ist, desto weiter ist das Maximum der Binomialverteilung \(B(200;\textcolor{200}{\textcolor{#e9b509}{p_1}})\) nach „rechts" verschoben und desto geringer sind die Wahrscheinlichkeiten im Annahmebereich \(\textcolor{#0087c1}{A = \{0;1;2; \dots\; 131\}}\). Deshalb wählt man für den Nachweis \(P(\text{Fehler 2. Art}) > 50\;\%\) einen Wert für \(\textcolor{#e9b509}{p_1}\), der in der Nähe von \(p_0 = 0{,}6\) liegt. Der nächstmögliche im Tafelwerk (TW) tabellarisierte Wert ist \(\textcolor{#e9b509}{p_1 = 0{,}65}\). Damit ergibt sich:
\[P(\text{Fehler 2. Art}) = P_{\textcolor{#e9b509}{0{,}65}}^{200}(Y \textcolor{#0087c1}{\leq 131}) \overset{\text{TW}}{=} 0{,}58520 \approx 58{,}5\,\% > 50\,\%\]
Tatsächlich ist \(\textcolor{#e9b509}{p_1 = 0{,}65}\) der einzige Wert, mit dem der Nachweis gelingt, denn bereits für \(\textcolor{#e9b509}{p_1 = \frac{2}{3} \approx 0{,}67}\) ist die Wahrscheinlichkeit für den Fehler 2. Art deutlich kleiner als 50 %, wie die nachfolgenden Histogramme veranschaulichen.
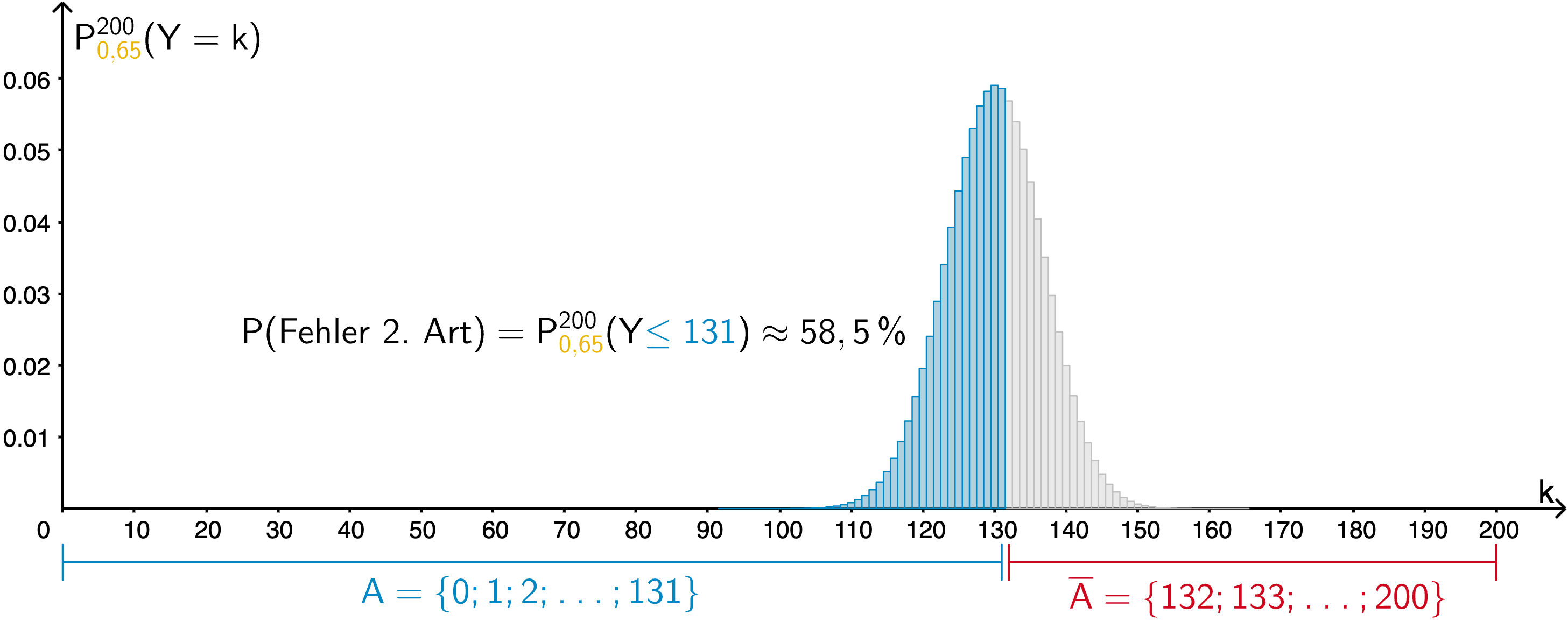
Wahrscheinlichkeit für den Fehler 2. Art unter der Annahme \(\textcolor{#e9b509}{p_1 = 0{,}65}\)
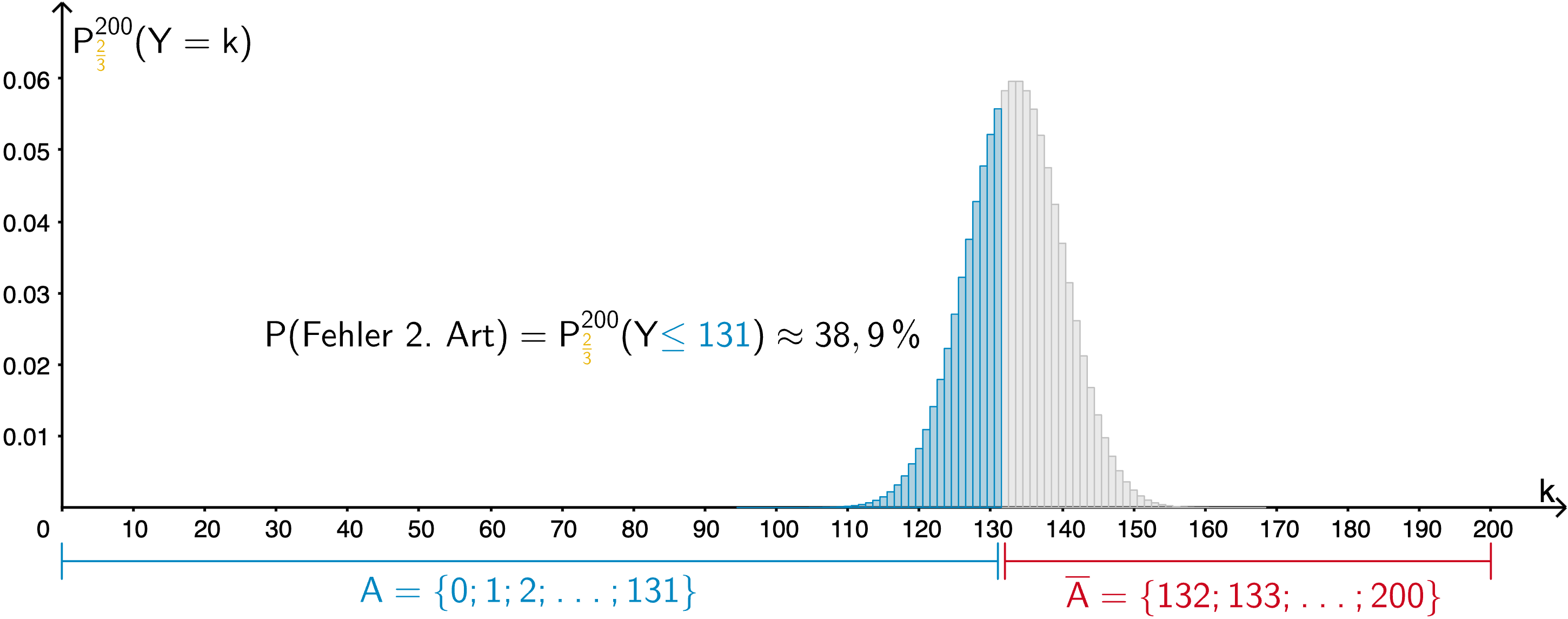
Wahrscheinlichkeit für den Fehler 2. Art unter der Annahme \(\textcolor{#e9b509}{p_1 = \frac{2}{3}}\)
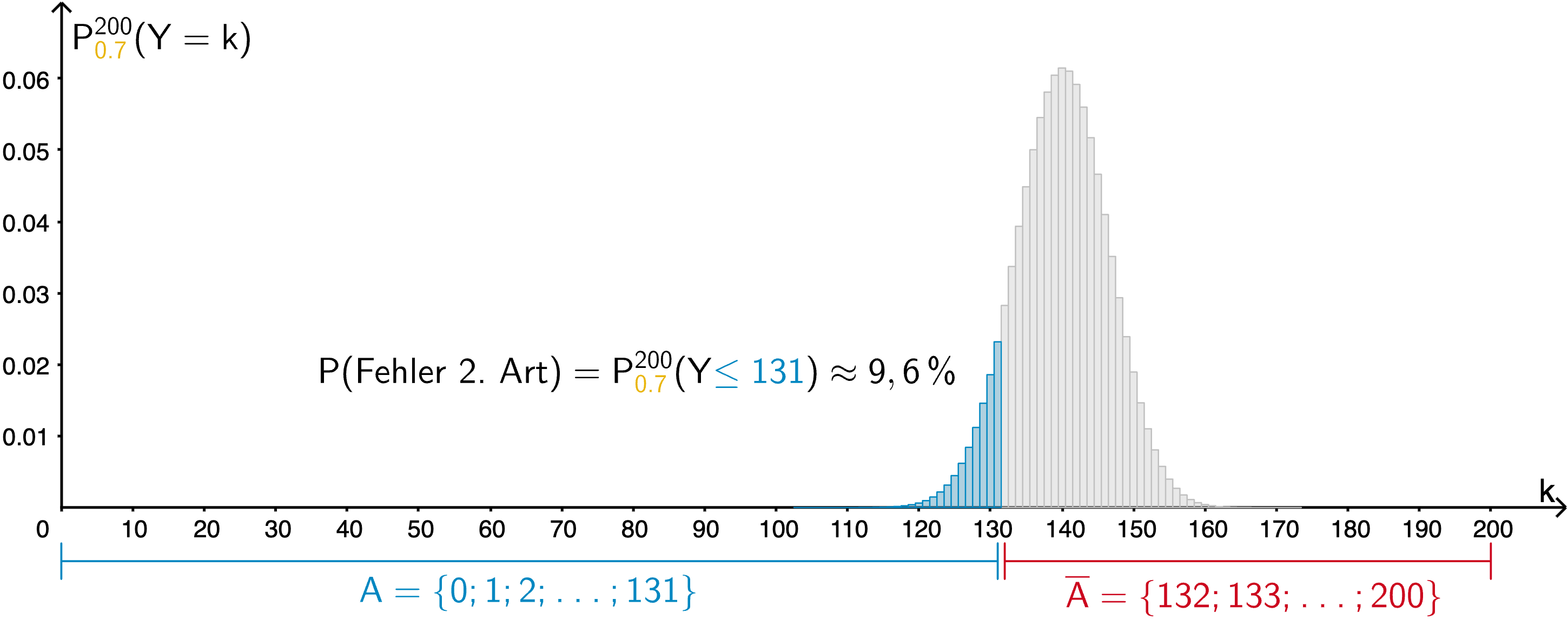
Wahrscheinlichkeit für den Fehler 2. Art unter der Annahme \(\textcolor{#e9b509}{p_1 = 0{,}7}\)


