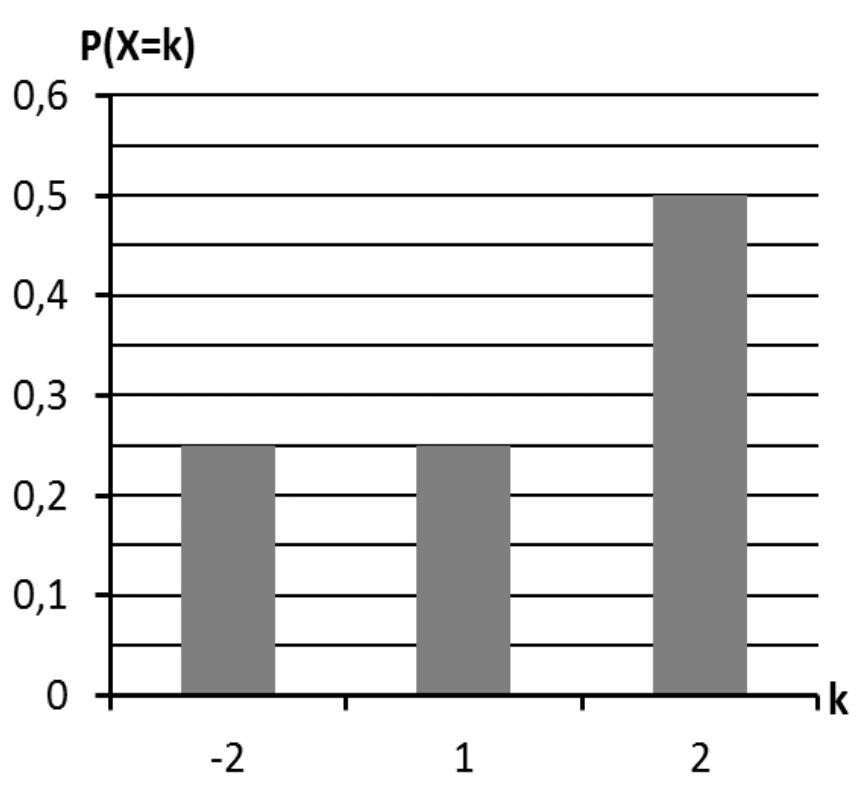
Für ein Zufallsexperiment wird eine Zufallsgröße \(X\) festgelegt, welche die drei Werte -2, 1 und 2 annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von \(X\) dargestellt.
Ermitteln Sie mithilfe der Abbildung den Erwartungswert der Zufallsgröße \(X\).
(2 BE)
Lösung zu Teilaufgabe 2a
Erwartungswert einer Zufallsgröße
Der Abbildung entnimmt man folgende Wahrscheinlichkeiten:
\[P(X = -2) = 0{,}25\]
\[P(X = 1) = 0{,}25\]
\[P(X = 2) = 0{,}5\]
Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) in Tabellenform:
| \(X = x_{i}\) | \(-2\) | \(1\) | \(2\) |
| \(P(X = x_{i})\) | \(0{,}25\) | \(0{,}25\) | \(0{,}5\) |
Erwartungswert \(E(X)\) der Zufallsgröße \(X\) berechnen:
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*} E(X) &= (-2) \cdot 0{,}25 + 1 \cdot 0{,}25 + 2 \cdot 0{,}5 \\[0.8em] &= -0{,}5 + 0{,}25 + 1 \\[0.8em] &= 0{,}75 \end{align*}\]
