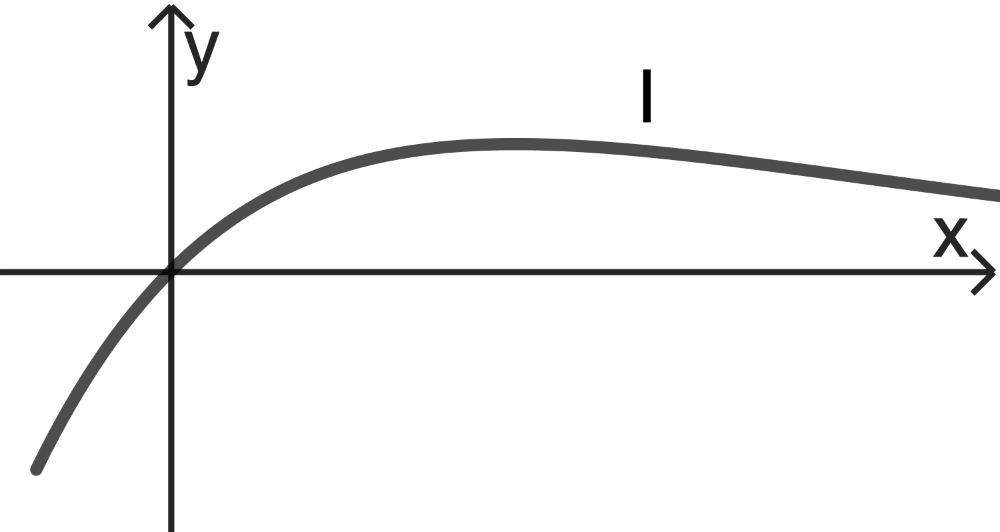
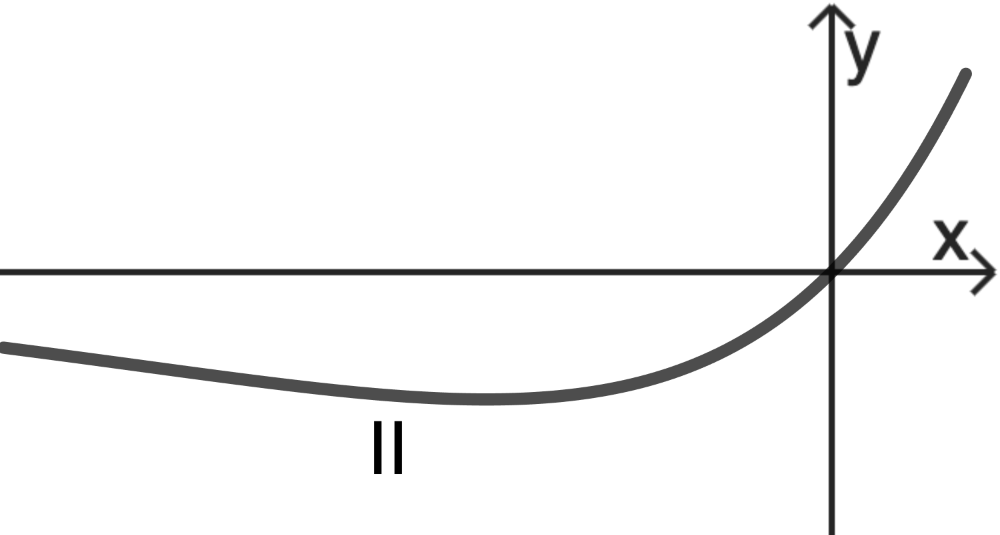
Die abgebildeten Graphen I und II sind Graphen der Schar; einer der beiden gehört zu einem positiven Wert von \(a\). Entscheiden Sie, welcher Graph dies ist, und begründen Sie Ihre Entscheidung.
(3 BE)
Lösung zu Teilaufgabe 3b


Die abgebildeten Graphen unterscheiden sich hinsichtlich ihres Verhaltens für \(x \to -\infty\) bzw. \(x \to +\infty\).
Für \(a > 0\) gilt:
\[\lim \limits_{x\,\to\,-\infty}f_a(x) = \lim \limits_{x\,\to\,-\infty}\; \textcolor{#0087c1}{\underset{\to\,-\infty}{x}} \cdot \underbrace{e^{\textcolor{#cc071e}{\overset{\to\,-\infty}{ax}}}}_{\to\,0} = 0^-\]
\[\lim \limits_{x\,\to\,+\infty}f_a(x) = \lim \limits_{x\,\to\,+\infty}\; \textcolor{#0087c1}{\underset{\to\,+\infty}{x}} \cdot \underbrace{e^{\textcolor{#cc071e}{\overset{\to\,+\infty}{ax}}}}_{\to\,+\infty} = +\infty\]
Da die Funktionen \(f_a\) für jeden Wert von \(a\) genau eine Extremstelle besitzen (vgl. Angabe Aufgabe 3), kommt für dieses Verhalten im Unendlichen ausschließlich Graph II in Frage.
Anmerkung
Als Begründung ist eine Grenzwertbetrachtung ausreichend, beispielsweise für \(x \to +\infty\). Der Verweis auf die einzige Extremstelle ist für eine eindeutige Begründung wichtig.


