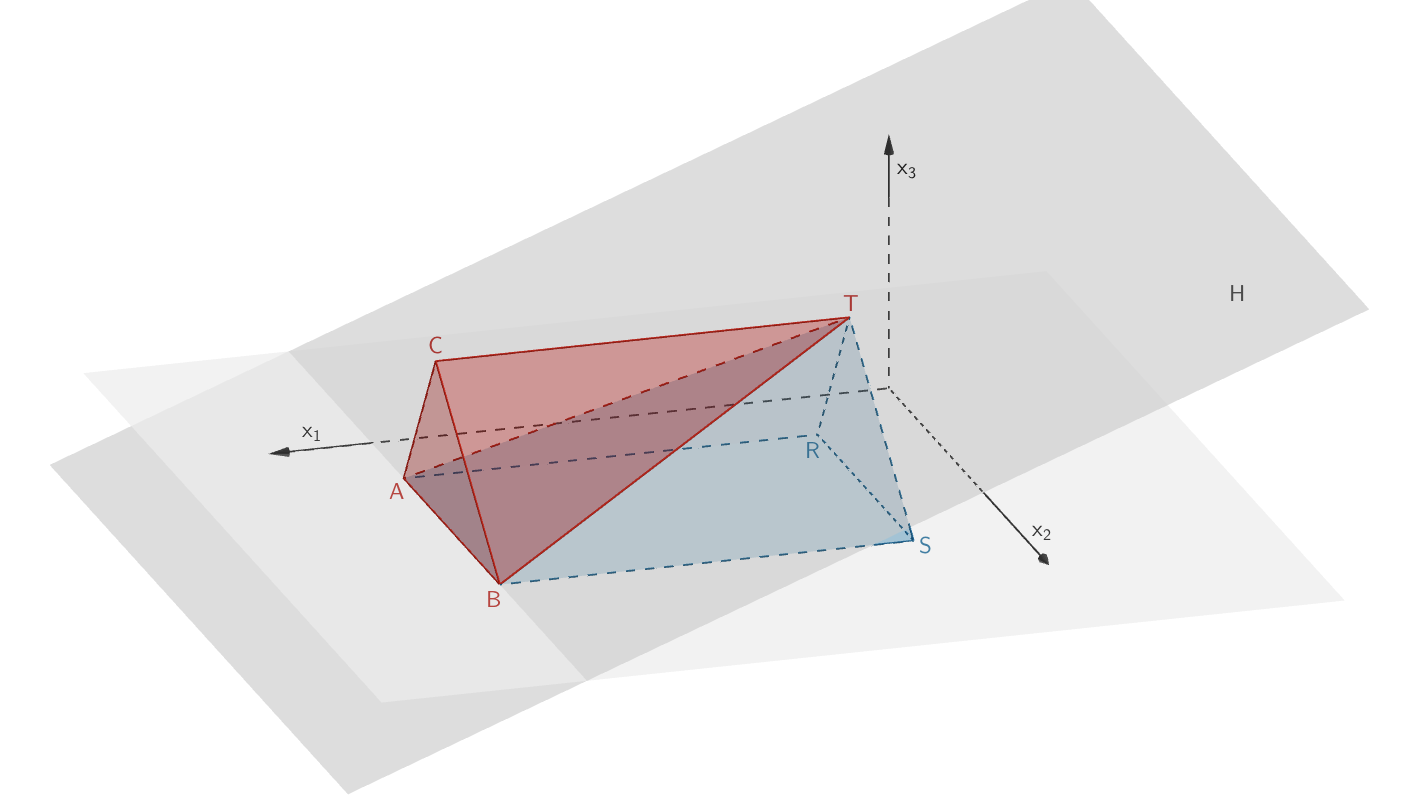
Die Punkte \(A\), \(B\) und \(T\) legen die Ebene \(H\) fest; diese zerlegt das Prisma ebenfalls in zwei Teilkörper. Beschreiben Sie die Form eines der beiden Teilkörper. Begründen Sie, dass die beiden Teilkörper nicht volumengleich sind.
(3 BE)
Lösung zu Teilaufgabe e
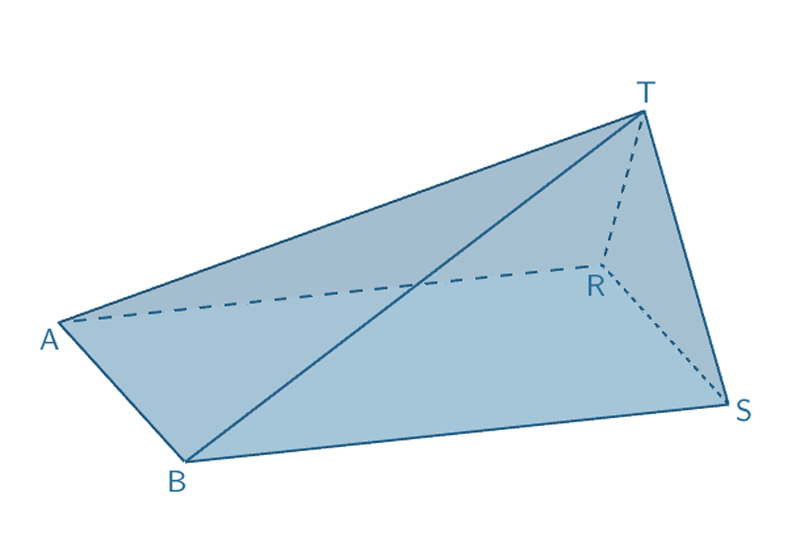
Die Ebene \(H\) zerlegt das Prisma \(ABCRST\) in die Teilkörper: Pyramide \(ABCT\) und Pyramide \(ABSRT\,\).
Form der Pyramiden
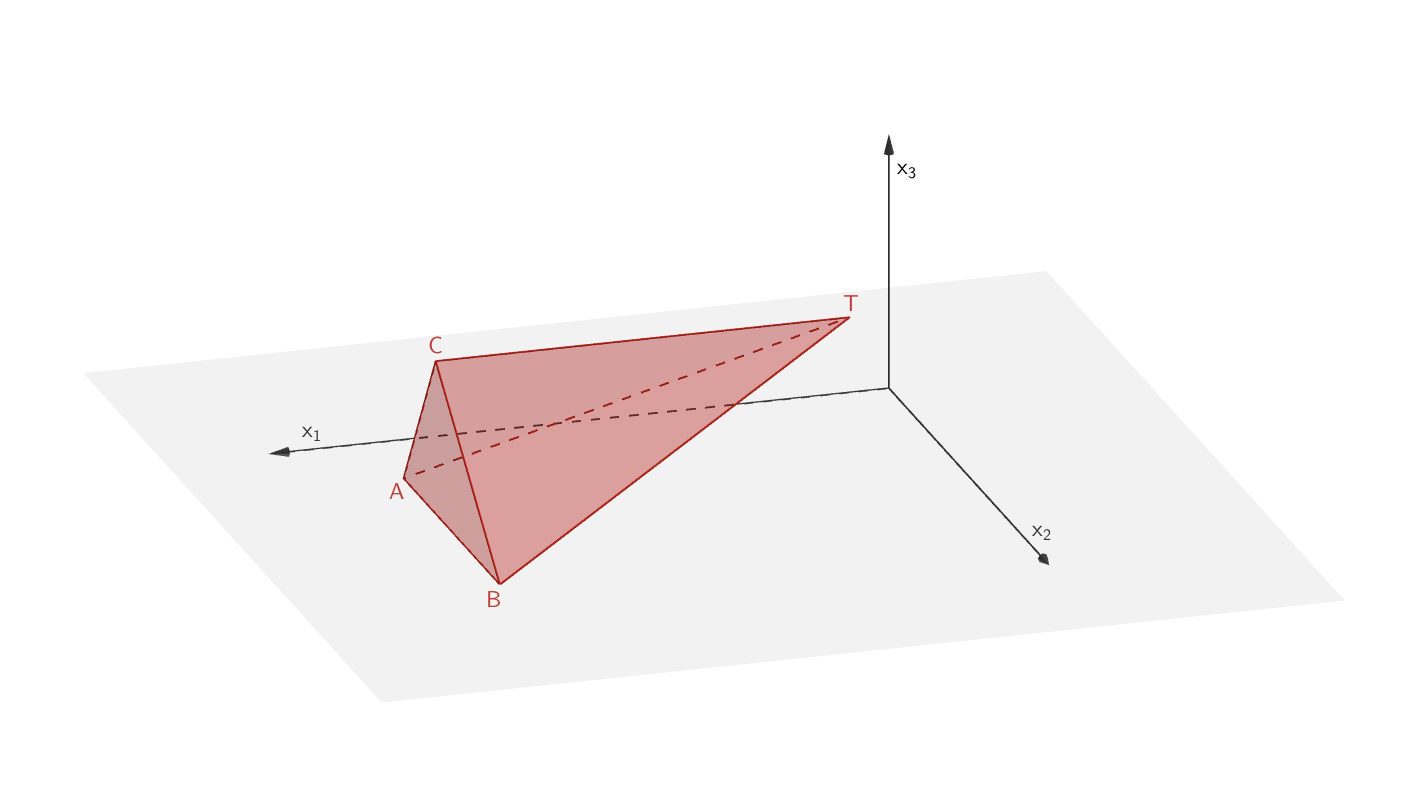
Die Pyramide \(ABCT\) ist eine dreiseitige Pyramide mit der Grundfläche \(ABC\) und der Höhe \([CT]\,\).
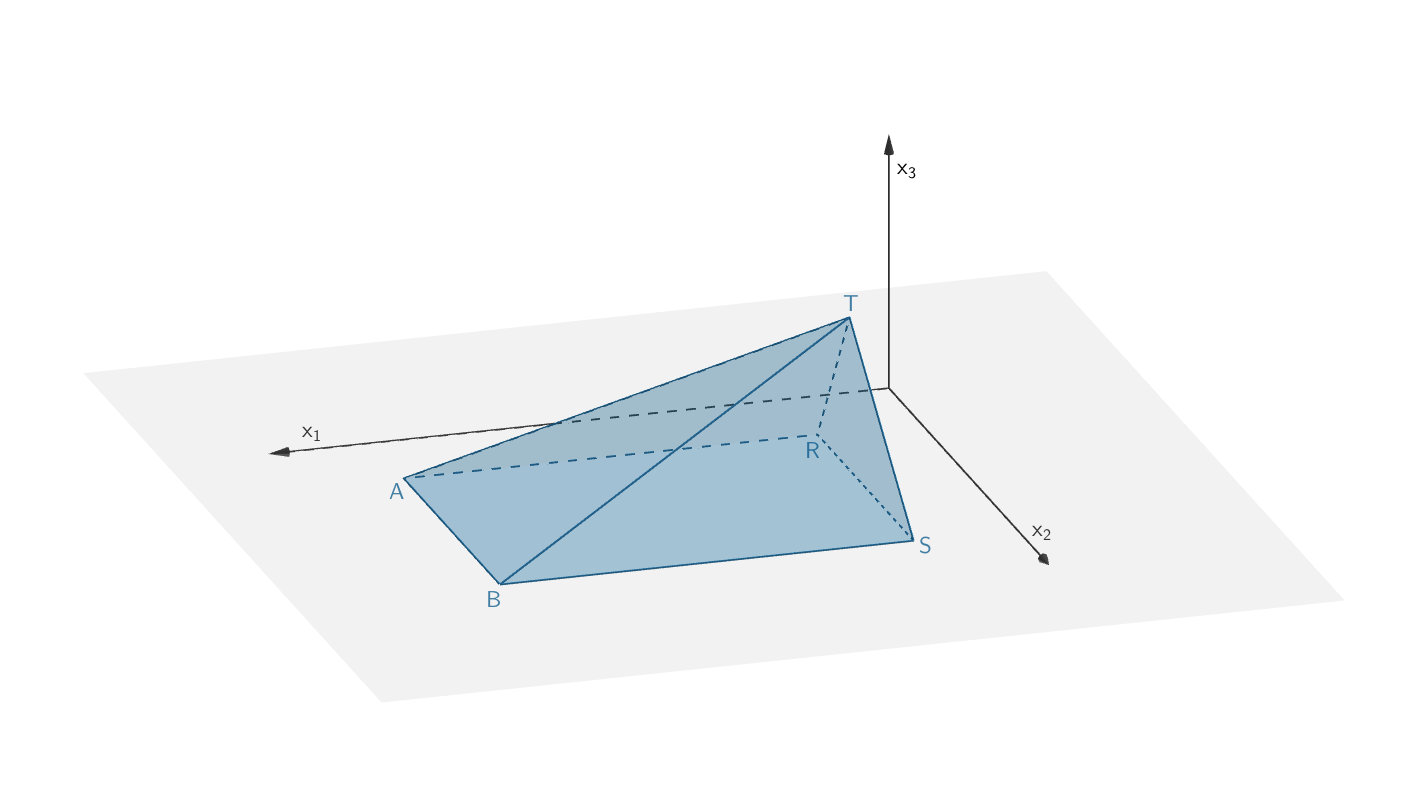
Die Pyramide \(ABSRT\) ist eine vierseitige Pyramide mit der Grundfläche \(ABSR\,\). Die Höhe der Pyramide legt der Abstand \(d\,(T;x_1x_2\text{-Ebene})\) des Punktes \(T\) von der \(x_1x_2\)-Ebene fest.
Begründung, dass die Pyramiden nicht volumengleich sind
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
Volumen der Pyramide \(ABCT\,\):
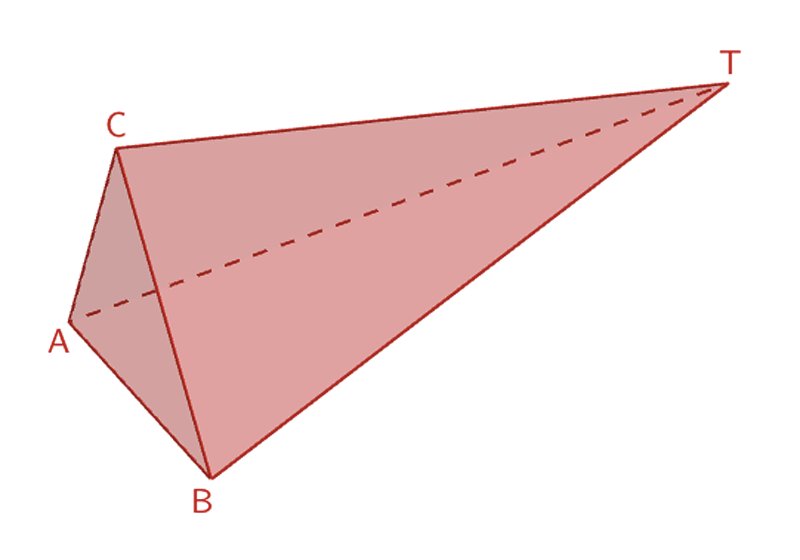
\[\begin{align*}V_{ABCT} &= \frac{1}{3} \cdot \underbrace{A_{ABC} \cdot \overline{CT}}_{V_{\,\text{Prisma}}} \\[0.8em] &= \frac{1}{3} \cdot V_{ABCRST}\end{align*}\]
Volumen der Pyramide \(ABSRT\,\):
\[\Longrightarrow \quad V_{ABSRT} = \frac{2}{3} \cdot V_{ABCRST}\]
\(\Longrightarrow \quad\) Die beiden Teilkörper sind nicht volumengleich.