Zufallsgröße
Eine Zufallsgröße oder Zufallsvariable \(X\) ist eine Funktion, die jedem Ergebnis \(\omega\) des Ergebnisraums \(\Omega\) eines Zufallsexperiments eine reelle Zahl \(x\) zuordnet.
\(X \colon \omega \mapsto X(\omega)\,\) mit \(\,\omega \in \Omega\,\) und \(\,X(\omega) \in \mathbb R\)
Die Funktionswerte \(x = X(\omega)\) heißen Werte der Zufallsgröße \(X\).
Zufallsgrößen werden üblicherweise mit lateinischen Großbuchstaben \(X, Y, Z, ...\) gekennzeichnet. Welche Werte \(x\) eine Zufallsgröße \(X\) annehmen kann, hängt vom jeweiligen Zufallsexperiment ab.
Beispiel:
Ein regelmäßiges Tetraeder (Körper mit vier gleichseitigen dreieckigen Seitenflächen, vgl. Abbildung), dessen Seitenflächen die Augenzahlen 1 bis 4 tragen, wird zweimal geworfen. Es wird die Augenzahl der Fläche notiert, auf die das Tetraeder fällt. Die Zufallsgröße \(X\) gibt die Summe der Augenzahlen an.
| \(\omega\) |
\((11)\)
\(\quad\)
\(\quad\)
\(\quad\)
|
\((12)\)
\((21)\)
\(\quad\)
\(\quad\)
|
\((13)\)
\((22)\)
\((31)\)
\(\quad\)
|
\((14)\)
\((23)\)
\((32)\)
\((41)\)
|
\(\quad\)
\((24)\)
\((33)\)
\((42)\)
|
\(\quad\)
\(\quad\)
\((34)\)
\((43)\)
|
\(\quad\)
\(\quad\)
\(\quad\)
\((44)\)
|
| \(X(\omega)\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) |
Ergebnisse \(\omega\) und zugehörige Werte \(x = X(\omega)\) der Zufallsgröße \(X\): „Summe der Augenzahlen"
Wahrscheinlichkeitsverteilung einer Zufallsgröße
Neben den Werten, die eine Zufallsgröße annehmen kann, ist vor allem die Wahrscheinlichkeit \(P\) dafür, dass eine Zufallsgröße \(X\) einen bestimmten Wert annimmt von Bedeutung.
Wahrscheinlichkeitsverteilung einer Zufallsgröße
Die Wahrscheinlichkeitsverteilung oder Wahrscheinlichkeitsfunktion \(W\) einer Zufallsgröße \(X\) ordnet jedem Wert \(x_{i} \;(i = 1, 2, ..., n)\) der Zufallsgröße \(X\) die Wahrscheinlichkeit \(P(X = x_{i}) = p_{i}\) zu.
\[W \colon x_{i} \mapsto P(X = x_{i})\]
| \(x_{i}\) | \(x_{1}\) | \(x_{2}\) | \(\dots\) | \(x_{n}\) |
| \(P(X = x_{i})\) | \(p_{1}\) | \(p_{2}\) | \(\dots\) | \(p_{n}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\)
Es gilt: \(p_{1} + p_{2} + \dots + p_{n} = \sum \limits_{i = 1}^{n} P(X = x_{i}) = 1\)
Mithilfe einer Verteilungstabelle, einem Stabdiagramm oder einem Histogramm lässt sich die Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\) veranschaulichen.
Beispiel:
Betrachtet wird die Zufallsgröße \(X\): „Summe der Augenzahlen" bei zweimaligem Werfen des Tetraeders (vgl. Beispiel oben).
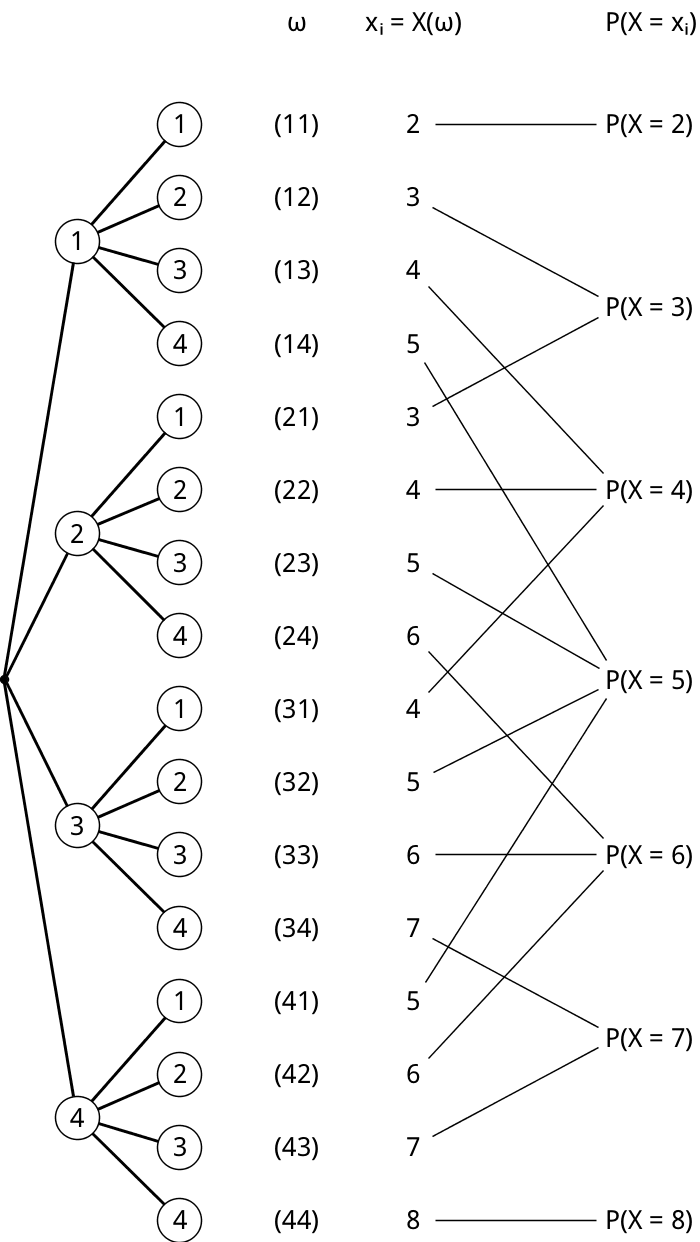
Veranschaulichung des Zufallsexperiments mithilfe eines Baumdiagramms: Ergebnisse \(\omega\) und zugehörige Werte \(x_{i} = X(\omega)\) sowie Wahrscheinlichkeiten \(P(X = x_{i})\)
Die Wahrscheinlichkeit, mit dem Tetraeder eine beliebige Augenzahl 1, 2, 3 oder 4 zu werfen, beträgt jeweils \(\frac{1}{4}\).
Die Wahrscheinlichkeit für ein beliebiges Ergebnis \(\omega\) nach zweimaligem Werfen beträgt \(\frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16}\).
Mithilfe der 1. bzw. 2. Pfadregel ergeben sich folgende Wahrscheinlichkeiten \(P(X = x_{i})\) (vgl. Abiturskript - 3.1.4 Baumdiagramm und Vierfeldertafel, Pfadregeln):
\[P(X = 2) = P(\{11\}) = \frac{1}{16}\]
\[P(X = 3) = P(\{12\}) + P(\{21\}) = \frac{1}{16} + \frac{1}{16} = \frac{2}{16}\]
\[\begin{align*}P(X = 4) &= P(\{13\}) + P(\{22\}) + P(\{31\}) \\[0.8em] &= \frac{1}{16} + \frac{1}{16} + \frac{1}{16} \\[0.8em] &= \frac{3}{16}\end{align*}\]
\[\begin{align*}P(X = 5) &= P(\{14\}) + P(\{23\}) + P(\{32\}) + P(\{41\}) \\[0.8em] &= \frac{1}{16} + \frac{1}{16} + \frac{1}{16} + \frac{1}{16} \\[0.8em] &= \frac{4}{16}\end{align*}\]
\[\begin{align*}P(X = 6) &= P(\{24\}) + P(\{33\}) + P(\{42\}) \\[0.8em] &= \frac{1}{16} + \frac{1}{16} + \frac{1}{16} \\[0.8em] &= \frac{3}{16}\end{align*}\]
\[P(X = 7) = P(\{34\}) + P(\{43\}) = \frac{1}{16} + \frac{1}{16} = \frac{2}{16}\]
\[P(X = 8) = P(\{44\}) = \frac{1}{16}\]
Veranschaulichung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mithilfe einer Verteilungstabelle:
| \(x_{i}\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) |
| \(P(X = x_{i})\) | \(\dfrac{1}{16}\) | \(\dfrac{2}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{4}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{2}{16}\) | \(\dfrac{1}{16}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Summe der Augenzahlen"
Probe:
Die Summe der Wahrscheinlichkeiten \(P(X = x_{i})\) aller Werte \(x_{i}\) der Zufallsgröße \(X\) ist gleich Eins.
\[\sum \limits_{i = 1}^{n} P(X = x_{i}) = \frac{1}{16} + \frac{2}{16} + \frac{3}{16} + \frac{4}{16} + \frac{3}{16} + \frac{2}{16} + \frac{1}{16} = \frac{16}{16} = 1\]
Veranschaulichung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mithilfe eines Stabdiagramms:
Bei einem Stabdiagramm gibt die Länge der Stäbe die Werte der Wahrscheinlichkeiten \(P(X = x_{i})\) an. Die Breite der Stäbe spielt keine Rolle.
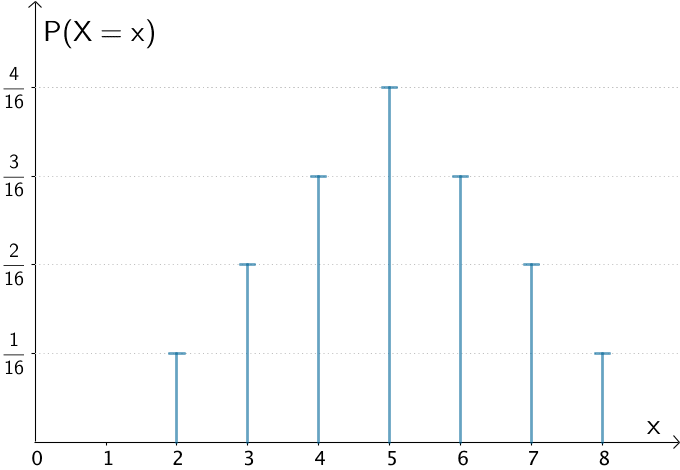
Stabdiagramm der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Summe der Augenzahlen"
Veranschaulichung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mithilfe eines Histogramms:
Bei einem Histogramm stellt der Flächeninhalt von Rechtecken die Werte der Wahrscheinlichkeiten \(P(X = x_{i})\) dar. Ist die Breite der Rechtecke 1, entsprechen die Wahrscheinlichkeit \(P(X = x_{i})\) den Höhen der Rechtecke.
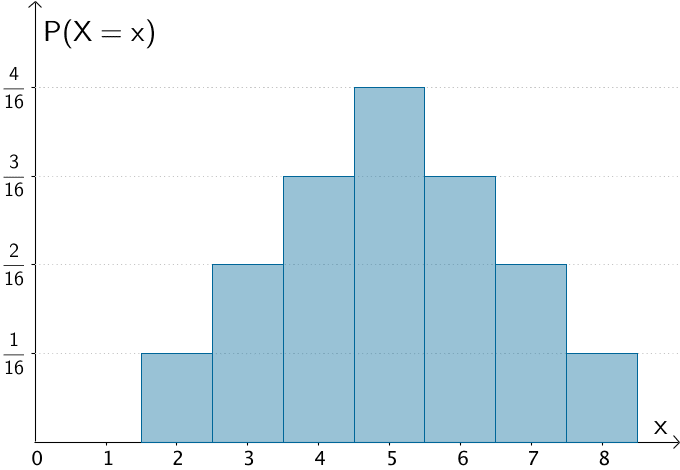
Histogramm der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Summe der Augenzahlen"
Mithilfe der Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\) wurde bisher die Wahrscheinlichkeit dafür betrachtet, dass die Zufallsgröße \(X\) einen bestimmten Wert \(x_{i}\) annimmt.
Die kumulative Verteilungsfunktion einer Zufallsgröße \(X\) beschreibt die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen Wert annimmt, der kleiner oder gleich einer vorgegebenen reellen Zahl \(x\) ist.
Kumulative Verteilungsfunktion einer Zufallsgröße
Die kumulative Verteilungsfunktion \(F\) einer Zufallsgröße \(X\) ordnet jeder reellen Zahl \(x\) die Wahrscheinlichkeit \(P(X \leq x)\) zu.
\[F \colon x \mapsto P(X \leq x)\]
Eigenschaften der kumulativen Verteilungsfunktion \(F\):
\[\lim \limits_{x \, \to \, -\infty} F(x) = 0; \quad \lim \limits_{x \, \to \, +\infty} F(x) = 1\]
\(F(x)\) ist eine monoton wachsende Funktion mit \(0 \leq F(x) \leq 1\).
Die Wahrscheinlichkeit \(P(a < X \leq b)\) dafür, dass die Zufallsgröße \(X\) einen Wert aus dem Intervall \(]a;b]\) annimmt, lässt sich als Differenz \(F(b) - F(a)\) berechnen.
Der Graph der kumulativen Verteilungsfunktion \(F\) einer Zufallsgröße \(X\) ist der Graph einer „Treppenfunktion". Die Werte \(x_{i}\) der Zufallsgröße \(X\) sind die Sprungstellen. Die Höhe des Sprungs an einer Sprungstelle \(x_{i}\) beträgt \(P(X = x_{i})\).
Beispiel:
Betrachtet wird die Zufallsgröße \(X\): „Summe der Augenzahlen" bei zweimaligem Werfen des Tetraeders (vgl. Beispiel oben).
Ausgehend von der bereits vorliegenden Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) lässt sich die kumulative Verteilungsfunktion \(F\) der Zufallsgröße \(X\) in Form einer Tabelle und graphisch veranschaulichen.
| \(x_{i}\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) |
| \(P(X = x_{i})\) | \(\dfrac{1}{16}\) | \(\dfrac{2}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{4}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{2}{16}\) | \(\dfrac{1}{16}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Summe der Augenzahlen"
Berechnung der Funktionswerte \(F(x_{i}) = P(X \leq x_{i})\) der kumulativen Verteilungsfunktion \(F\):
\[F(2) = P(X \leq 2) = \frac{1}{16}\]
\[F(3) = P(X \leq 3) = P(X = 2) + P(X = 3) = \frac{1}{16} + \frac{2}{16} = \frac{3}{16}\]
\[\begin{align*}F(4) &= P(X \leq 4) \\[0.8em] &= P(X = 2) + P(X = 3) + P(X = 4) \\[0.8em] &= \frac{1}{16} + \frac{2}{16} + \frac{3}{16} \\[0.8em] &= \frac{6}{16} \end{align*}\]
\[\begin{align*}F(5) &= P(X \leq 5) \\[0.8em] &= P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) \\[0.8em] &= \frac{1}{16} + \frac{2}{16} + \frac{3}{16} + \frac{4}{16} \\[0.8em] &= \frac{10}{16} \end{align*}\]
\[\begin{align*}F(6) &= P(X \leq 6) \\[0.8em] &= P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) \\[0.8em] &= \frac{1}{16} + \frac{2}{16} + \frac{3}{16} + \frac{4}{16} + \frac{3}{16} \\[0.8em] &= \frac{13}{16} \end{align*}\]
\[\begin{align*}F(7) =\quad &P(X \leq 7) \\[0.8em] = \quad &P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) \, + \\[0.8em] + \; &P(X = 6) + P(X = 7) \\[0.8em] = \quad &\frac{1}{16} + \frac{2}{16} + \frac{3}{16} + \frac{4}{16} + \frac{3}{16} + \frac{2}{16} \\[0.8em] = \quad &\frac{15}{16} \end{align*}\]
\[\begin{align*}F(8) =\quad &P(X \leq 8) \\[0.8em] = \quad &P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) \, + \\[0.8em] + \; &P(X = 6) + P(X = 7) + P(X = 8) \\[0.8em] = \quad &\frac{1}{16} + \frac{2}{16} + \frac{3}{16} + \frac{4}{16} + \frac{3}{16} + \frac{2}{16} + \frac{1}{16} \\[0.8em] = \quad &\frac{16}{16} \\[0.8em] = \quad &1 \end{align*}\]
| \(x_{i}\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) |
| \(F(x_{i}) = P(X \leq x_{i})\) | \(\dfrac{1}{16}\) | \(\dfrac{3}{16}\) | \(\dfrac{6}{16}\) | \(\dfrac{10}{16}\) | \(\dfrac{13}{16}\) | \(\dfrac{15}{16}\) | \(\dfrac{16}{16} = 1\) |
Kumulativen Verteilungsfunktion \(F\) der Zufallsgröße \(X\): „Summe der Augenzahlen" in Form einer Tabelle
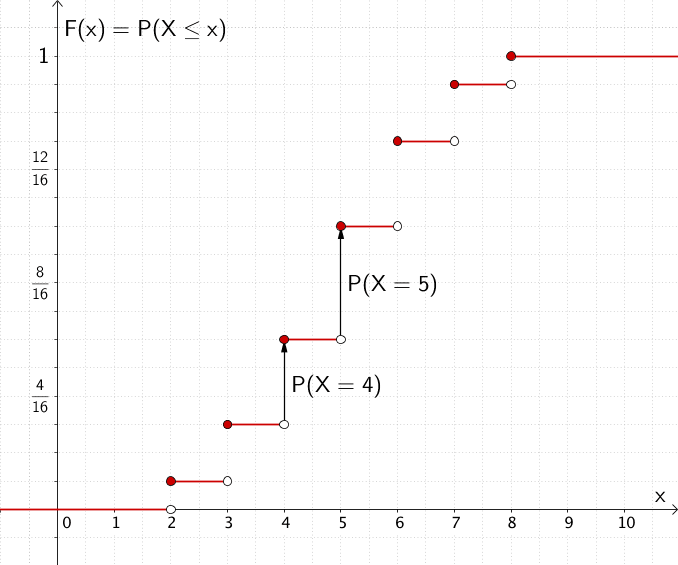
Graph der kumulativen Verteilungsfunktion \(F\) der Zufallsgröße \(X\): „Summe der Augenzahlen"
Beispielaufgabe
Ein Händler für Raumausstattung und Innendekoration erhält eine Lieferung von 20 Vasen eines bestimmten Designs. Dem Händler ist bekannt, dass versehentlich drei beschädigte Vasen mitgeliefert wurden. Zu Kontrollzwecken entnimmt er der Lieferung fünf Vasen. Die Zufallsgröße \(X\) beschreibt die Anzahl der entnommenen beschädigten Vasen.
a) Erstellen Sie eine Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) und veranschaulichen Sie diese mithilfe eines Stabdiagramms.
b) Berechnen Sie die Wahrscheinlichkeit dafür, dass der Händler mindestens eine beschädigte Vasen entnimmt.
a) Verteilungstabelle und Stabdiagramm der Wahrscheinlichkeitsverteilung von \(X\)
\(X\): „Anzahl der entnommenen beschädigten Vasen"
Bei drei mitgelieferten beschädigten Vasen kann die Zufallsgröße \(X\) die Werte \(x_{1} = 0\), \(x_{2} = 1\), \(x_{3} = 2\) und \(x_{4} = 3\) annehmen.
Berechnung der Wahrscheinlichkeiten \(P(X = x_{i})\) der Werte \(x_{i}\) der Zufallsgröße \(X\):
Da die Vasen der Lieferung entnommen werden und die Reihenfolge der Entnahme keine Rolle spielt, kann das Urnenmodell „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge" zugrunde gelegt werden (vgl. Abiturskript - 3.2.2 Berechnung von Wahrscheinlichkeiten).
\[P(X = 0) = \frac{\displaystyle \binom{3}{0} \cdot \binom{17}{5}}{\displaystyle \binom{20}{5}} = \frac{91}{228} \approx 0{,}40\]
\[P(X = 1) = \frac{\displaystyle \binom{3}{1} \cdot \binom{17}{4}}{\displaystyle \binom{20}{5}} = \frac{105}{228} \approx 0{,}46\]
\[P(X = 2) = \frac{\displaystyle \binom{3}{2} \cdot \binom{17}{3}}{\displaystyle \binom{20}{5}} = \frac{30}{228} \approx 0{,}13\]
\[P(X = 3) = \frac{\displaystyle \binom{3}{3} \cdot \binom{17}{2}}{\displaystyle \binom{20}{5}} = \frac{2}{228} \approx 0{,}01\]
Probe:
Die Summe der Wahrscheinlichkeiten \(P(X = x_{i})\) muss gleich Eins sein.
\[\sum \limits_{i = 1}^{n = 4} P(X = x_{i}) = \frac{91}{228} + \frac{105}{228} + \frac{30}{228} + \frac{2}{228} = \frac{228}{228} = 1\]
| \(x_{i}\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(P(X = x_{i})\) | \(\dfrac{91}{228}\) | \(\dfrac{105}{228}\) | \(\dfrac{30}{228}\) | \(\dfrac{2}{228}\) |
Verteilungstabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Anzahl der entnommenen beschädigten Vasen"
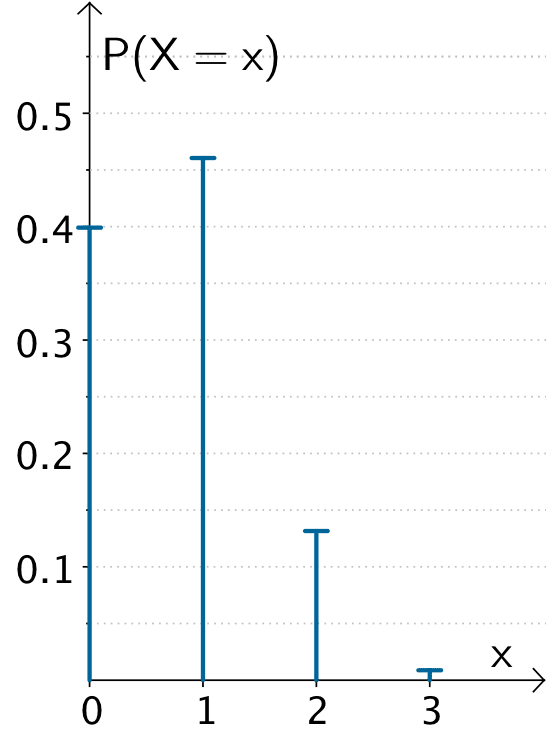
Stabdiagramm der Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\): „Anzahl der entnommenen beschädigten Vasen"
b) Wahrscheinlichkeit, dass der Händler mindestens eine beschädigte Vase entnimmt
Wahrscheinlichkeitsberechnungen der Form „mindestens 1 Treffer" vereinfachen sich durch die Betrachtung des Gegenereignisses. Das Gegenereignis zu „mindestens eine beschädigte Vase" lautet „keine beschädigte Vase".
\[P(X \geq 1) = 1 - P(X = 0) = 1 - \frac{91}{228} = \frac{137}{228} \approx 0{,}60 = 60\,\%\]


