Geben Sie den Term einer in \(\mathbb R\) definierten Funktion an, die eine Stammfunktion, aber keine Integralfunktion von \(f\) ist.
(2 BE)
Lösung zu Teilaufgabe 1h
Zusammenhang Integralfunktion - Stammfunktion
Anmerkung:
Der Term der gesuchten Stammfunktion ist lediglich anzugeben. Jede Erklärung kann entfallen.
\[f(x) = 2e^{-x} \cdot \left( 2e^{-x} - 1 \right); \; D_{f} = \mathbb R\]
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Gemäß dem Hauptsatz der Differential- und Integralrechnung (HDI) ist jede Integralfunktion von \(f\) eine Stammfunktion von \(f\). Umgekehrt gilt dies nicht, denn jede Integralfunktion von \(f\) hat mindestens eine Nullstelle, aber nicht jede Stammfunktion von \(f\) hat eine Nullstelle.
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Die Menge aller Stammfunktionen von \(f\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int f(x) dx = F(x) + C\). Dabei bezeichnet \(F(x)\) den Funktionsterm einer Stammfunktion von \(f\) und \(C\) die sogenannte Integrationskonstante mit \(C \in \mathbb R\).
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Die Integrationskonstante \(C\) bewirkt eine Verschiebung des Graphen einer Stammfunktion von \(f\) in \(y\)-Richtung.
Aus Teilaufgabe 1d ist bekannt, dass die Stammfunktion \(F\) der Funktion \(f\) mit \(F(x) = 2e^{-x} - 2e^{-2x}\) keinen größeren Wert als \(0{,}5\) annehmen kann. Zudem wurde in Teilaufgabe 1e der Graph der Stammfunktion \(F\) mit dem absoluten Hochpunkt \(HoP(\ln{2}|0{,}5)\) gezeichnet.
Verschiebt man nun den Graphen \(G_{F}\) der Stammfunktion \(F\) um mehr als \(0{,}5\) Einheiten in Richtung der negativen \(y\)-Achse, liegt der absolute Hochpunkt des Graphen der entstehenden Stammfunktion unterhalb der \(x\)-Achse. Die Stammfunktion hat somit keine Nullstelle und ist daher keine Integralfunktion von \(f\).
Beispielsweise ist die Funktion \(F_{-1}(x) = F(x) - 1 = 2e^{-x} -2e^{-2x} - 1\) eine Stammfunktion, aber keine Integralfunktion von \(f\).
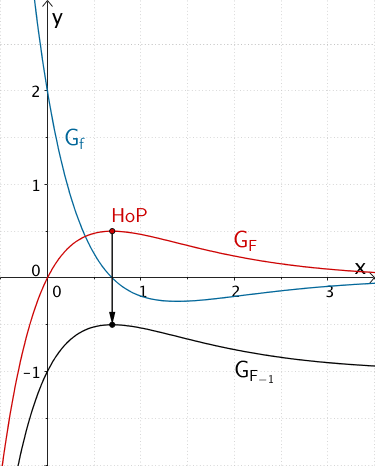
Der Graph \(G_{F_{-1}}\) der Stammfunktion \(F_{-1} \colon x \mapsto 2e^{-x} -2e^{-2x} - 1\) von \(f\) verläuft vollständig unterhalb der \(x\)-Achse. Die Stammfunktion \(F_{-1}\) hat somit keine Nullstelle und ist daher keine Integralfunktion von \(f\).


