Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ \(k \colon x \mapsto 5 \cdot \cos(c \cdot x)\) mit \(c \in \mathbb R\) und Definitionsbereich \(D_{k} = [-5;5]\), bei der offensichtlich Bedingung II erfüllt ist.
Bestimmen Sie \(c\) so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittfläche des Tunnels.
(zur Kontrolle: \(c = \frac{\pi}{10}\), Inhalt der Querschnittfläche: \(\frac{100}{\pi}\) m²)
(5 BE)
Lösung zu Teilaufgabe 2a
Allgemeine Kosinusfunktion, Flächeninhaltsberechnung durch Integration
\[k(x) = 5 \cdot \cos(c \cdot x); \; c \in \mathbb R, \, D_{k} = [-5;5]\]
Bestimmung von \(c\), sodass Bedingung I erfüllt ist
1. Lösungsansatz: Betrachtung der Periode \(p\) der Kosinusfunktion \(k\)
Bedingung I:
Breite des Tunnelbodens: b = 10 m
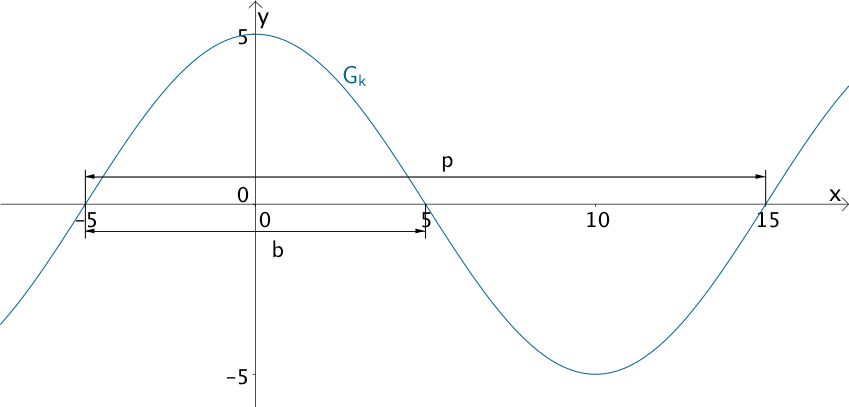
Damit Bedingung I mit b = 10 m erfüllt ist, muss die Periode \(p\) der Kosinusfunktion \(k \colon x \mapsto 5 \cdot \cos(c \cdot x)\) doppelt so lang sein wie die Breite b des Tunnelbodens.
\[p = 2 \cdot b = 2 \cdot 10 = 20\]
Für die Länge der Periode \(p\) der Kosinusfunktion \(k\) gilt:
Allgemeine Kosinusfunktion
\[f(x) = a \cdot \cos(bx + c) + d = a \cdot \cos \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[p = \frac{2\pi}{\vert c \vert}\]
Damit lässt sich der Wert für \(c\) berechnen:
\[\begin{align*}p = \frac{2\pi}{\vert c \vert} \quad \Longleftrightarrow \quad \vert c \vert &= \frac{2\pi}{p} \\[0.8em] &= \frac{2\pi}{20} \\[0.8em] &= \frac{\pi}{10} \end{align*}\]
\[\Longrightarrow \quad c = \frac{\pi}{10} \enspace \vee \enspace c = -\frac{\pi}{10}\]
Wegen \(\displaystyle \cos\left( -\frac{\pi}{10} \cdot x \right) = \cos\left( \frac{\pi}{10} \cdot x \right)\) (vgl. Merkhilfe) ist die Betrachtung von \(\displaystyle c = \frac{\pi}{10}\) ausreichend.
Die Modellierung des Querschnitts der Tunnelwand unter Verwendung der Kosinusfunktion \(\displaystyle k \colon x \mapsto 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right)\) mit \(D_{k} = [-5;5]\) erfüllt Bedingung I (und Bedingung II).
2. Lösungsansatz: Betrachtung der Nullstellen der Kosinusfunktion \(k\)
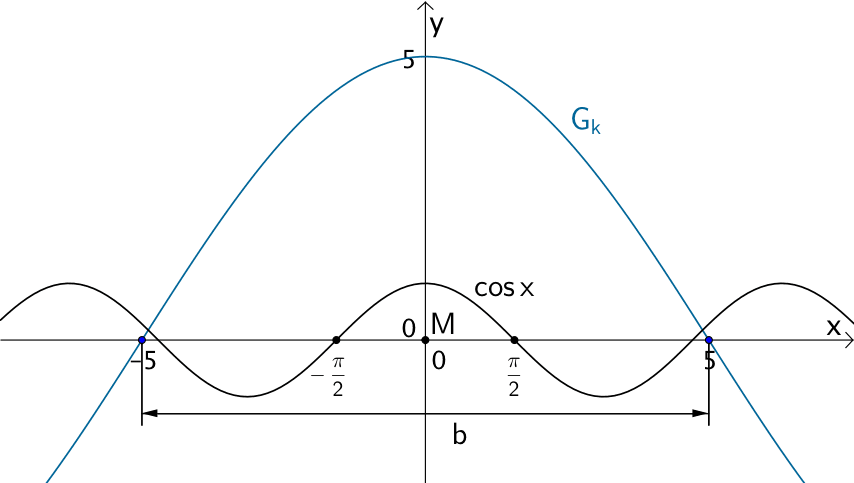
Die Kosinusfunnktion \(x \mapsto \cos{x}\) besitzt für \(x = (2k + 1) \cdot \dfrac{\pi}{2}\) mit \(k \in \mathbb Z\) Nullstellen (ungeradzahliges Vielfaches von \(\dfrac{\pi}{2}\)). In nächster Nähe des Koordinatenursprungs \(M\) sind dies die Nullstellen \(x = -\dfrac{\pi}{2}\) und \(x = \dfrac{\pi}{2}\).
Damit Bedingung I mit b = 10 m erfüllt ist, muss die Kosinusfunktion \(k\) in nächster Nähe von \(M\) die Nullstellen \(x = -5\) und \(x = 5\) haben.
Damit ergibt sich:
\[k(x) = 5 \cdot \cos(c \cdot x); \; c \in \mathbb R, \, D_{k} = [-5;5]\]
\[\begin{align*} k(-5) = 0 \quad \Longrightarrow \quad \cos(c \cdot (-5)) &= 0 \\[0.8em] \Longrightarrow \quad c \cdot (-5) &= -\frac{\pi}{2} & &| : (-5) \\[0.8em] c &= \frac{\pi}{10} \end{align*}\]
bzw.
\[\begin{align*} k(5) = 0 \quad \Longrightarrow \quad \cos(c \cdot 5) &= 0 \\[0.8em] \Longrightarrow \quad c \cdot 5 &= -\frac{\pi}{2} & &| : 5 \\[0.8em] c &= \frac{\pi}{10} \end{align*}\]
Die Modellierung des Querschnitts der Tunnelwand unter Verwendung der Kosinusfunktion \(\displaystyle k \colon x \mapsto 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right)\) mit \(D_{k} = [-5;5]\) erfüllt Bedingung I (und Bedingung II).
Inhalt der Querschnittfläche des Tunnels
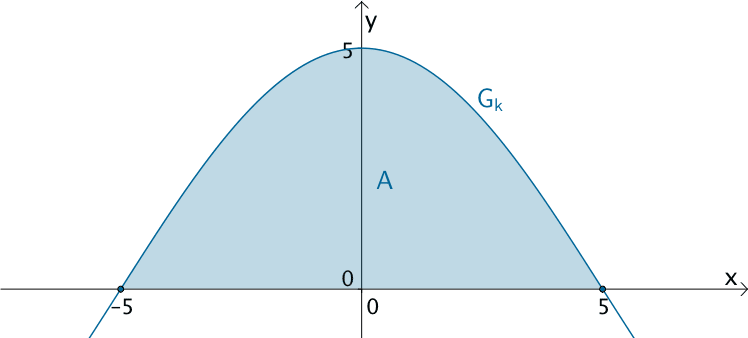
Der Inhalt der Querschnittfläche des Tunnels entspricht dem Flächeninhalt \(A\) des Flächenstücks, das der Graph der Kosinusfunktion \(\displaystyle k \colon x \mapsto 5 \cdot \cos \left( \frac{\pi}{10} \cdot x \right); \; D_{k} = [-5;5]\) mit der \(x\)-Achse einschließt.
Das bestimmte Integral \(\displaystyle \int_{-5}^{5} k(x)\, dx\) errechnet die Maßzahl des Flächeninhalts \(A\).
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A = \int_{-5}^{5} k(x)\, dx = K(5) - K(-5)\]
Stammfunktion \(K\) der Integrandenfunktion \(k\) bilden:
\[k(x) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right); \; D_{k} = [-5;5]\]
Wichtige unbestimmte Integrale:
\[\int f(ax + b)\;dx = \frac{1}{a}F(ax +b) + C\]
Dabei ist \(F\) eine Stammfunktion von \(f\).
\[\int \cos x\;dx = \sin x + C\]
(vgl. Merkhilfe)
\[\begin{align*}K(x) &= 5 \cdot \frac{1}{\frac{\pi}{10}} \cdot \sin\left( \frac{\pi}{10} \cdot x \right) + C \\[0.8em] &= 5 \cdot \frac{10}{\pi} \cdot \sin\left( \frac{\pi}{10} \cdot x \right) + C \\[0.8em] &= \frac{50}{\pi} \cdot \sin\left( \frac{\pi}{10} \cdot x \right) + C \end{align*}\]
Die Funktion \(\displaystyle K \colon x \mapsto \frac{50}{\pi} \cdot \sin\left( \frac{\pi}{10} \cdot x \right)\) ist eine Stammfunktion der Integrandenfunktion \(k\) (für \(C = 0\)).
Flächeninhalt \(A\) berechnen:
\[\begin{align*} A &= \int_{-5}^{5} 5 \cdot \cos \left( \frac{\pi}{10} \cdot x \right) dx \\[0.8em] &= \left[ \frac{50}{\pi} \cdot \sin\left( \frac{\pi}{10} \cdot x \right)\ \right]_{-5}^{5} \\[0.8em] &= \frac{50}{\pi} \cdot \left[ \sin\left( \frac{\pi}{10} \cdot x \right)\ \right]_{-5}^{5} \\[0.8em] &= \frac{50}{\pi} \cdot \left[ \sin \left( \frac{10}{\pi} \cdot 5 \right) - \sin \left( \frac{\pi}{10} \cdot (-5) \right) \right] \\[0.8em] &= \frac{50}{\pi} \cdot \left[ \sin \left( \frac{\pi}{2} \right) - \sin \left( -\frac{\pi}{2} \right) \right] \\[0.8em] &= \frac{50}{\pi} \cdot \left( 1 - (-1) \right) \\[0.8em] &= \frac{100}{\pi} \end{align*}\]
Der Inhalt der Querschnittfläche des Tunnels beträgt \(\frac{\sf{100}}{\sf{\pi}}\,\sf{m}^{2}\).


