Die Punkte \(O(0|0|0)\), \(P(5|2|2)\) und \(Q(-2|4|-2)\) legen die Grundfläche \(OPQ\) der Pyramide \(OPQS\) mit dem Volumeninhalt 20 VE (Volumeneinheiten) fest. Die Spitze \(S\) der Pyramide \(OPQS\) liegt auf der positiven \(x_{3}\)-Achse.
a) Bestimmen Sie eine Gleichung der Ebene \(E\) in Normalenform, in der die Grundfläche \(OPQ\) liegt.
(mögliches Ergebnis: \(E \colon -2x_{1} + x_{2} + 4x_{3} = 0\))
b) Berechnen Sie den Neigungswinkel der Grudfläche \(QPS\) gegenüber der Horizontalen.
c) Berechnen Sie die Koordinaten der Pyramidenspitze \(S\).
d) Die Menge aller Pyramidenspitzen \(S^{*}\), sodass der Volumeninhalt der Pyramiden \(OPQS^{*}\) stets 20 VE beträgt, ist gegeben durch die Ebene \(F\). Ermitteln Sie eine Gleichung der Ebene \(F\) in Normalenform.
a) Gleichung der Ebene \(E\) in Normalenform
Die Punkte \(O(0|0|0)\), \(P(5|2|2)\) und \(Q(-2|4|-2)\) legen die Grundfläche \(OPQ\) fest, welche in der Ebene \(E\) liegt.
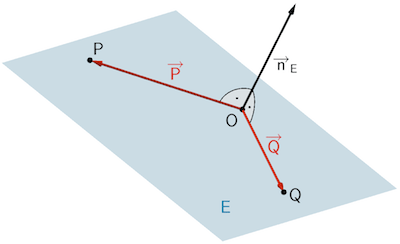
Das Vektorprodukt (Kreuzprodukt) zweier linear unabhängiger Vektoren, beispielsweise der Ortsvektoren \(\overrightarrow{P}\) und \(\overrightarrow{Q}\), liefert einen Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\). Als Aufpunkt wählt man einen der gegebenen Punkte \(O\), \(P\) oder \(Q\). Damit lässt sich eine Gleichung der Ebene in Normalenform angeben.
Der Ansatz kann mithilfe der Normalenform in Vektordarstellung oder in Koordinatendarstellung erfolgen (vgl. Abiturskript - 2.2.3 Ebenengleichung in Normalenform). Die Aufgabenstellung nennt als mögliches Ergebnis eine Gleichung der Ebene \(E\) in Normalenform in Koordinatendarstellung.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
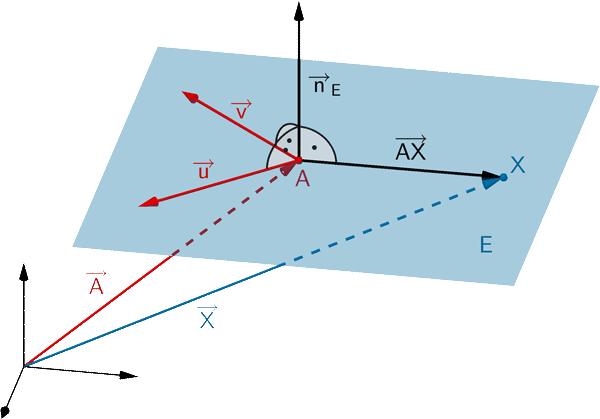
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ermitteln:
\(P(5|2|2)\), \(Q(-2|4|-2)\)
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} \overrightarrow{P} \times \overrightarrow{Q} &= \begin{pmatrix} 5 \\ 2 \\ 2 \end{pmatrix} \times \begin{pmatrix} -2 \\ 4 \\ -2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix}2 & \cdot & (-2) & - & 2 & \cdot & 4 \\ 2 & \cdot & (-2) & - & 5 & \cdot & (-2) \\ 5 & \cdot & 4 & - & 2 & \cdot & (-2) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -12 \\ 6 \\ 24 \end{pmatrix} \\[0.8em] &= 6 \cdot \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix}\]
Gleichung der Ebene \(E\) in Normalenform formulieren:
1. Möglichkeit: Ansatz mit der Normalenform in Vektordarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Es sei \(O\) der Aufpunkt der Ebene \(E\).
\[\overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix}, \; O(0|0|0)\]
\[\begin{align*} &E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{O}) = 0 \\[0.8em] &E \colon \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right] = 0 \end{align*}\]
Ggf. wandelt man die Ebenengleichung in Normalenform in Vektordarstellung in die Koordinatendarstellung um. Hierfür wird das Skalarprodukt ausmultipliziert.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right] &= 0 \\[0.8em] (-2) \cdot (x_{1} - 0) + 1 \cdot (x_{2} - 0) + 4 \cdot (x_{3} - 0) &= 0 \\[0.8em] -2x_{1} + x_{2} + 4x_{3} &= 0\end{align*}\]
\[\Longrightarrow \quad E \colon -2x_{1} + x_{2} + 4x_{3} = 0\]
2. Möglichkeit: Ansatz mit der Normalenform in Koordinatendarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Es sei \(O\) der Aufpunkt der Ebene \(E\).
\[\overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix}, \; O(0|0|0)\]
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
\[E \colon -2x_{1} + x_{2} + 4x_{3} + n_{0} = 0\]
\[\begin{align*} O \in E \colon 3 \cdot 0 + 2 \cdot 0 + 4 \cdot 0 + n_{0} &= 0 \\[0.8em] n_{0} &= 0 \end{align*}\]
\[\Longrightarrow \quad E \colon -2x_{1} + x_{2} + 4x_{3} = 0\]
b) Neigungswinkel der Grundfläche \(QPS\) gegenüber der Horizontalen
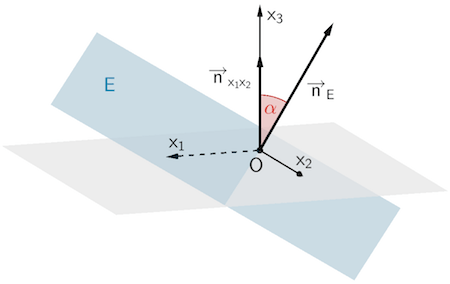
Der Neigungswinkel der Grundfläche \(OPQ\) gegenüber der Horizontale entspricht dem Schnittwinkel der Ebene \(E\) und der \(x_{1}x_{2}\)-Ebene. Dieser ist gleich dem spitzen Winkel \(\alpha\), den ein Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und ein Normalenvektor \(\overrightarrow{n}_{x_{1}x_{2}}\) der \(x_{1}x_{2}\)-Ebene festlegen.
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
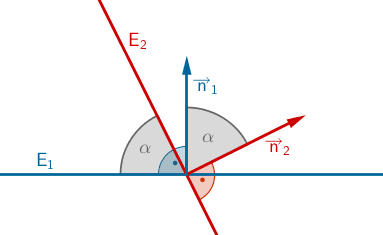
Beispielsweise ist \(\overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\) ein Normalenvektor der \(x_{1}x_{2}\)-Ebene.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \alpha &= \frac{\left| \overrightarrow{n}_{E} \circ \overrightarrow{n}_{x_{1}x_{2}} \right|}{\left| \overrightarrow{n}_{E} \right| \cdot \left| \overrightarrow{n}_{x_{1}x_{2}} \right|} \\[0.8em] &= \frac{\left| \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert (-2) \cdot 0 + 1 \cdot 0 + 4 \cdot 1 \vert}{\sqrt{(-2)^{2} + 1^{2} + 4^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{4}{\sqrt{21}} \\[0.8em] &= \frac{4\sqrt{21}}{21} & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[3.2em] \alpha &\approx 29{,}2^{\circ}\end{align*}\]
Die Grundfläche \(OPQ\) ist gegenüber der Horizontalen um ca. 29,2° geneigt.
c) Koordinaten der Pyramidenspitze \(S\)
Die Pyramidenspitze \(S\) liegt auf der positiven \(x_{3}\)-Achse (vgl. Angabe).
\(\Longrightarrow \quad S(0|0|s_{3})\) mit \(s_{3} > 0\)
Anmerkung:
Die nachfolgend vorgestellten Lösungsansätze sind möglich, weil bereits zwei Koordinaten des Punktes \(S\) bekannt sind.
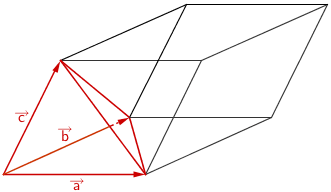
1. Lösungsansatz: Spatprodukt anwenden
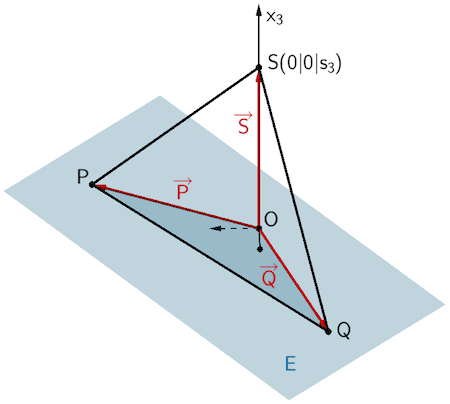
Das Volumen der dreiseitigen Pyramide \(OPQS\) lässt sich mithilfe des Spatprodukts berechnen. Der Volumeninhalt beträgt 20 VE (vgl. Angabe).
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
\[\begin{align*}V_{OPQS} &= 20 \\[0.8em] \frac{1}{6} \cdot \left| \overrightarrow{S} \circ ( \overrightarrow{P} \times \overrightarrow{Q}) \right| &= 20 \end{align*}\]
Der Vektor \(\overrightarrow{P} \times \overrightarrow{Q} = \begin{pmatrix} -12 \\ 6 \\ 24 \end{pmatrix}\) ist aus Teilaufgabe a bereits bekannt.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \frac{1}{6} \cdot \left| \begin{pmatrix} 0 \\ 0 \\ s_{3} \end{pmatrix} \circ \begin{pmatrix} -12 \\ 6 \\ 24 \end{pmatrix} \right| &= 20 \\[0.8em] \frac{1}{6} \cdot \vert| 0 \cdot (-12) + 0 \cdot 6 + s_{3} \cdot 24 \vert &= 20 &&| \; s_{3} > 0 \\[0.8em] \frac{1}{6} \cdot 24s_{3} &= 20 \\[0.8em] 4s_{3} &= 20 &&| : 4 \\[0.8em] s_{3} &= 5 \end{align*}\]
\[\Longrightarrow \quad S(0|0|5)\]
2. Lösungsansatz: Abstand Punkt - Ebene
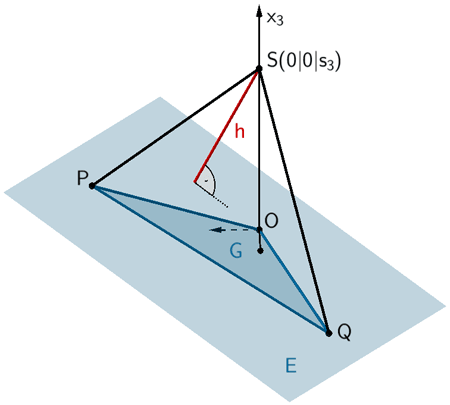
Das Lot der Spitze \(S\) auf die Ebene \(E\), in der die Grundfläche \(G\) (Dreieck \(OPQ\)) liegt, legt die Höhe \(h\) der Pyramide \(OPQS\) fest. Die Höhe \(h\) entspricht dem Abstand \(d(S;E)\) des Punktes \(S\) von der Ebene \(E\).
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[d(S;E) = h\]
Der Flächeninhalt der Grundfläche \(G\) lässt sich mithilfe des Vektorprodukts berechnen. Folglich kann bei bekanntem Volumeninhalt der Pyramide \(OPQS\) die Höhe \(h\) berechnet werden.
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\[V_{OPQS} = \frac{1}{3} \cdot G \cdot h \quad \Longleftrightarrow \quad h = \frac{3 \cdot V_{OPQS}}{G}\]
Die Formel für den Abstand \(d(S;E)\) wird aus der Hesseschen Normalenform der Ebene \(E\) abgeleitet. Damit liefert die Gleichung \(d(S;E) = h\) die \(x_{3}\)-Koordinate der Pyramidenspitze \(S\).
Flächeninhalt der Grundfläche \(G\) berechnen:
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
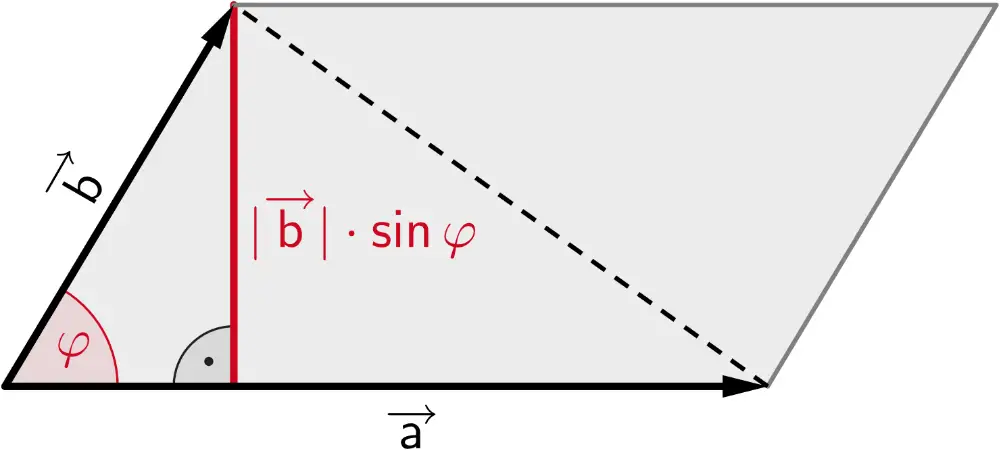
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\[\begin{align*} G &= A_{OPQ} \\[0.8em] &= \frac{1}{2} \cdot \vert \overrightarrow{P} \times \overrightarrow{Q} \vert \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} -12 \\ 6 \\ 24 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{(-12)^{2} + 6^{2} + 24^{2}} \\[0.8em] &= 3\sqrt{21} \end{align*}\]
Höhe \(h\) der Pyramide \(OPQS\) berechnen:
\[h = \frac{3 \cdot V_{OPQS}}{G} = \frac{\cancel{3} \cdot 20}{\cancel{3}\sqrt{21}} = \frac{20}{\sqrt{21}} \enspace \left( = \frac{20\sqrt{21}}{21} \right)\]
Hessesche Normalenform der Ebene \(E\) ermitteln:
Die Hessesche Normalenform \(E_{HNF}\) der Ebene \(E\) entsteht durch Division der Gleichung der Ebene \(E\) in Normalenform durch den Betrag des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[E \colon -2x_{1} + x_{2} + 4x_{3} = 0\]
\(\vert \overrightarrow{n}_{E} \vert = \sqrt{21}\) (vgl. Teilaufgabe b)
\[E_{HNF} \colon \frac{-2x_{1} + x_{2} + 4x_{3}}{\sqrt{21}} = 0\]
Damit ergibt sich der Abstand \(d(S;E)\) des Punktes \(S(0|0|s_{3})\) von der Ebene \(E\) zu:
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[\begin{align*}d(S;E) &= \left| \frac{-2s_{1} + s_{2} + 4s_{3}}{\sqrt{21}} \right| \\[0.8em] &= \left| \frac{(-2) \cdot 0 + 0 + 4s_{3}}{\sqrt{21}} \right| &&| \; s_{3} > 0 \\[0.8em] &= \frac{4s_{3}}{\sqrt{21}} \end{align*}\]
\(x_{3}\)-Koordinate der Pyramidenspitze \(S\) berechnen:
\[\begin{align*} d(S;E) &= h \\[0.8em] \frac{4s_{3}}{\sqrt{21}} &= \frac{20}{\sqrt{21}} &&| \cdot \sqrt{21} \\[0.8em] 4s_{3} &= 20 &&| : 4 \\[0.8em] s_{3} &= 5 \end{align*}\]
\[\Longrightarrow \quad S(0|0|5)\]
d) Gleichung der Ebene \(F\) in Normalenform
Die Ebene \(F\) liegt im Abstand \(d(F;E) = h\) parallel zur Ebene \(E\). Dann beträgt der Volumeninhalt aller Pyramiden \(OPQS^{*}\) mit \(S^{*} \in F\) stets 20 VE, da bei gleicher Grundfläche \(G\) die Höhe \(h\) der Pyramiden konstant ist.
Ein Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) ist gegeben durch den Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[E \parallel E \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \overrightarrow{n}_{E} = \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix}\]
Die Pyramidenspitze \(S(0|0|5)\) liegt in der Ebene \(F\) und dient als Aufpunkt einer Gleichung der Ebene \(F\) in Normalenform. Die Gleichung kann in Normalenform in Vektordarstellung oder in Koordinatendarstellung angegeben werden.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung:
\[F \colon \begin{pmatrix} -2 \\ 1 \\ 4 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0 \\ 5 \end{pmatrix} \right] = 0\]
Gleichung der Ebene \(F\) in Normalenform in Koordinatendarstellung:
\[F \colon -2x_{1} + x_{2} + 4x_{3} + n_{0} = 0\]
\[\begin{align*}S(0|0|5) \in F \colon (-2) \cdot 0 + 0 + 4 \cdot 5 + n_{0} &= 0 \\[0.8em] 20 + n_{0} &= 0 &&| - 20 \\[0.8em] n_{0} &= -20 \end{align*}\]
\[\Longrightarrow \quad F \colon -2x_{1} + x_{2} + 4x_{3} - 20 = 0\]
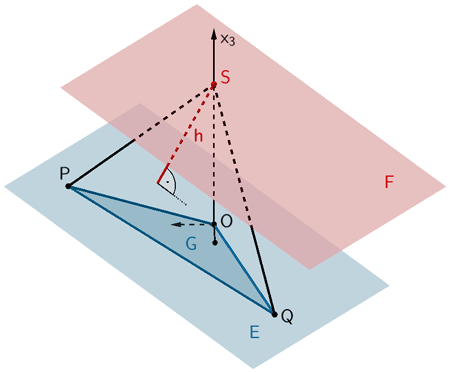
Ebene \(F \parallel E\) im Abstand \(d(F;E) = h\), welche die Menge aller Punkte \(S^{*}\) bildet, sodass das Volumen der Pyramiden \(OPQS^{*}\) stets 20 VE beträgt.

