Betrachtet wird eine Schar von Funktionen \(h_{k}\) mit \(k \in \mathbb R^{+}\), die sich nur in ihren jeweiligen Definitionsbereichen \(D_{k}\) unterscheiden.
Es gilt \(h_{k} \colon x \mapsto \cos{x}\) mit \(D_{k} = [0;k]\).
Abbildung 4 zeigt den Graphen der Funktion \(h_{7}\). Geben Sie den größtmöglichen Wert von \(k\) an, sodass die zugehörige Funktion \(h_{k}\) umkehrbar ist. Zeichnen Sie für diesen Wert von \(k\) den Graphen der Umkehrfunktion von \(h_{k}\) in Abbildung 4 ein und berücksichtigen Sie dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
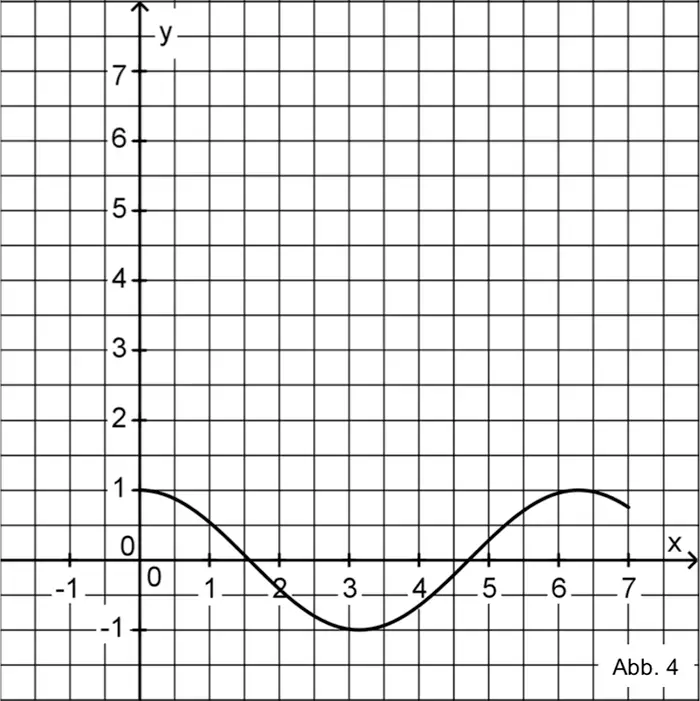
(3 BE)
Lösung zu Teilaufgabe 4a
\[k_{max} = \pi\]
Kriterien für die Umkehrbarkeit einer Funktion
Eine Funktion \(f\,\colon\,\mapsto f(x)\) mit der Definitionsmenge \(D_{f}\) und der Wertemenge \(W_{f}\) heißt umkehrbar, falls es zu jedem \(y \in W_{f}\) genau ein \(x \in D_{f}\) mit \(f(x) = y\) gibt.
Ist eine Funktion auf Ihrer Definitionsmenge oder einer Teilmenge streng monoton (steigend oder fallend), so ist sie dort umkehrbar.
Begründung (nicht verlangt)
Es gilt \(\cos{\pi} = -1\). Die Funktion \(h_{\pi}(x) = \cos{x}\) mit \(D_{\pi} = [0;\pi]\) ist streng monoton fallend und deshalb umkehrbar.
Graphische Begründung:
Jede zur \(x\)-Achse parallele Gerade mit der Gleichung \(y = c; \; c \in [-1;1]\) schneidet den Graphen der Funktion \(h_{\pi}(x) = \cos{x}\) mit \(D_{\pi} = [0;\pi]\) genau einmal. Somit gibt es zu jedem Wert der Wertemenge von \(h_{\pi}\) genau einen Wert der Definitionsmenge von \(h_{\pi}\) und die Funktion \(h_{\pi}\) ist folglich umkehrbar.
Zeichnung der Umkehrfunktion von \(h_{\pi}\)
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
![Zeichnung der Umkehrfunktion von hπ(x) = cos x mit Dπ = [0;π]](/images/stories/B2019_PT_A_A1/B2019_PT_A_A1_4a.png)
Der Graph \(\textcolor{#cc071e}{G_{h_{\pi}^{-1}}}\) der Umkehrfunktion von \(\textcolor{#0087c1}{h_{\pi}}\) entsteht durch Spiegelung des Graphen \(\textcolor{#0087c1}{G_{h_{\pi}}}\) an der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\). Dabei ist der Schnittpunkt von \(\textcolor{#0087c1}{G_{h_{\pi}}}\) mit der Winkelhalbierenden Fixpunkt der Spiegelung, sodass sich die Graphen \(\textcolor{#cc071e}{G_{h_{\pi}^{-1}}}\) und \(\textcolor{#0087c1}{G_{h_{\pi}}}\) auf der Winkelhalbierenden schneiden.


