Die von der Anlage produzierte elektrische Energie wird vollständig in das Stromnetz eingespeist. Der Hauseigentümer erhält für die eingespeiste elektrische Energie eine Vergütung von 10 Cent pro Kilowattstunde (kWh).
Die in \([4;20]\) definierte Funktion \(x \mapsto E(x)\) gibt die elektrische Energie in kWh an, die die Anlage am betrachteten Tag von 4:00 Uhr bis x Stunden nach Mitternacht in das Stromnetz einspeist.
Es gilt \(E'(x) = p(x)\) für \(x \in [4;20]\).
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für die Vergütung, die der Hauseigentümer für die von 10:00 Uhr bis 14:00 Uhr in das Stromnetz eingespeiste elektrische Energie erhält.
(3 BE)
Lösung zu Teilaufgabe 3d
\[x \mapsto E(x); D_{E} = [4;20]\]
\[E'(x) = p(x); x \in [4;20]\]
\(x\): Seit Mitternacht vergangene Zeit in Stunden (h)
\(E(x)\): In das Stromnetz eingespeiste elektrische Energie in Kilowattstunden (kWh)
\(E'(x) = p(x)\): Leistung in Kilowatt (kW) (momentane Änderungsrate von \(E(x)\))
Vergütung: 10 Cent pro kWh
![Fläche, die der Graph der Funktion p im Intervall [10;14] mit der x-Achse einschließt.](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_3d.png)
Die zwischen 10:00 Uhr und 14:00 Uhr in das Stromnetz eingespeiste elektrische Energie entspricht dem Flächeninhalt der Fläche, die \(G_{p}\) im Intervall \([10;14]\) mit der \(x\)-Achse einschließt. Das bestimmte Integral \(\displaystyle \textcolor{#0087c1}{\int_{10}^{14}p(x)dx}\) errechnet die Maßzahl des Flächeninhalts dieser Fläche. Näherungsweise ergibt sich durch „Kästchen zählen":
\[\textcolor{#0087c1}{\int_{10}^{14}p(x)dx} \approx \textcolor{#0087c1}{8} \cdot \textcolor{#0087c1}{4\;\text{kWh}} = 32\;\text{kWh}\]
Vergütung, die der Hauseigentümer erhält:
\[32\;\text{kWh} \cdot 10\;\frac{\text{Cent}}{\text{kWh}} = 320\;\text{Cent} = 3{,}20\;\text{Euro}\]
Ausführliche Erklärung (nicht verlangt)
Teilaufgabe 3d behandelt eine wichtige Anwendung der Integralrechnung.
Beschreibt eine Funktion \(f\) die momentane Änderungsrate einer Größe in Abhängigkeit von der Zeit \(t\), so errechnet das bestimmte Integral \(\displaystyle \int_{t_{1}}^{t_{2}}f(t)dt\) den Wert der Gesamtänderung der Größe im Zeitintervall \([t_{1};t_{2}]\).
Differentialquotient oder lokale bzw. momentane Änderungsrate
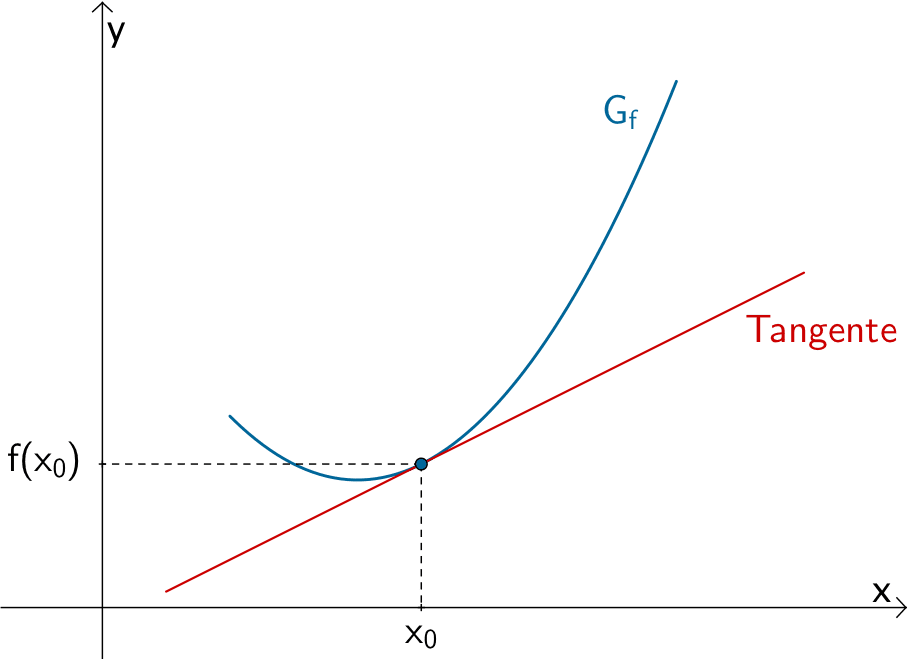
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Im vorliegenden Sachverhalt beschreibt die Funktion \(E'\) mit \(E'(x) = p(x)\) für \(x \in [4;20]\) die montane Änderungsrate von \(\boldsymbol{E(x)}\) (eingespeiste elektrische Energie) in Abhängigkeit von der Zeit \(x\) (in Stunden).
Dann errechnet das bestimmte Integral \(\displaystyle \int_{10}^{14}E'(x)dx\) den Wert der im Zeitintervall \([10;14]\) (in der Zeit von von 10:00 Uhr bis 14:00 Uhr) insgesamt in das Stromnetz eingespeisten elektrischen Energie.
Mit \(E'(x) = p(x)\) (vgl. Angabe) folgt:
\[\int_{10}^{14}E'(x)dx = \textcolor{#0087c1}{\int_{10}^{14}p(x)dx}\]
Das bestimmte Integral \(\displaystyle \textcolor{#0087c1}{\int_{10}^{14}p(x)dx}\) errechnet die Maßzahl des Flächeninhalts der Fläche, die der Graph der Funktion \(p\) im Intervall \([10;14]\) mit der \(x\)-Achse einschließt.
Mithilfe der Abbildung von \(G_{p}\) lässt sich der Flächeninhalt dieser Fläche näherungsweise durch „Kästchen zählen" ermitteln.
![Fläche, die der Graph der Funktion p im Intervall [10;14] mit der x-Achse einschließt.](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_3d.png)
Da \(x\) die seit Mitternacht vergangene Zeit in Stunden (h) bedeutet und \(y = p(x)\) die Leistung in Kilowatt (kW), entspricht der Flächeninhalt eines Kästchens einer elektrischen Energie von \(\textcolor{#0087c1}{2\;\text{h} \cdot 2\;\text{kW} = 4\;\text{kWh}}\).
Somit ergibt sich näherungsweise:
\[\textcolor{#0087c1}{\int_{10}^{14}p(x)dx} \approx \textcolor{#0087c1}{8} \cdot \textcolor{#0087c1}{4\;\text{kWh}} = 32\;\text{kWh}\]
\[32\;\text{kWh} \cdot 10\;\frac{\text{Cent}}{\text{kWh}} = 320\;\text{Cent} = 3{,}20\;\text{Euro}\]


