Geben Sie alle Werte von \(k\) an, für die der Graph von \(f_k\) und der Graph der Umkehrfunktion von \(f_k\) keinen gemeinsamen Punkt haben.
(2 BE)
Lösung zu Teilaufgabe 1h
\[k \in \;]-2;+\infty[\]
Ausführliche Erklärung (nicht verlangt)
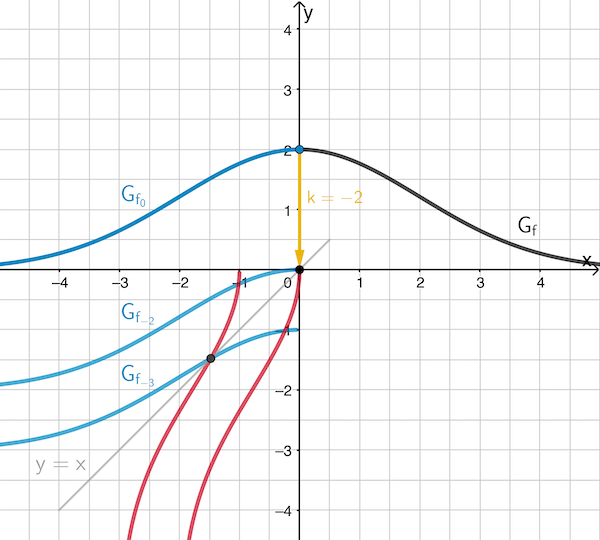
Allgemein gilt: Die Schnittpunkte des Graphen einer Funktion und des Graphen deren Umkehrfunktion liegen auf der Winkelhalbierenden des I. und III. Quadranten. Sie sind Fixpunkte der Spiegelung an der Winkelhalbierenden, durch die der Graph einer Umkehrfunktion aus dem Graphen einer Funktion hervorgeht.
Der Parameter \(k\) der Funktionenschar \(f_k\colon x \mapsto f(x) + k\) verschiebt für \(k \neq 0\) den Graphen von \(f_0\) in Richtung der \(y\)-Achse.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Der Graph von \(\textcolor{#0087c1}{f_0}\; (k = 0)\) endet mit \(D_{f_k} = ]-\infty;\textcolor{#0087c1}{0]}\) im Punkt \(\textcolor{#0087c1}{(0|2)}\) auf der \(y\)-Achse (vgl. Teilaufgabe 1a).
Für \(k > 0\) gibt es offensichtlich keinen gemeinsamen Punkt des Graphen von \(f_k\) und der Winkelhalbierenden.
Für \(\textcolor{#e9b509}{k = -2}\) endet der Graph der Funktion \(\textcolor{#0087c1}{f_{-2}}\) im Koordinatenursprung, durch den auch die Winkelhalbierende verläuft.
Für \(k < -2\) schneidet jeder Graph von \(f_k\) die Winkelhalbierende (vgl. Abbildung, Graph von \(\textcolor{#0087c1}{f_{-3}}\; (k = -3)\)).
Damit ist \(\textcolor{#e9b509}{k = -2}\) der größtmögliche Wert für \(\boldsymbol{k}\) für den der Graph von \(\textcolor{#0087c1}{f_k}\) und der Graph der Umkehrfunktion von \(\textcolor{#cc071e}{f_k}\) einen gemeinsamen Punkt haben.
Also haben der Graph von \(\textcolor{#0087c1}{f_k}\) und der Graph der Umkehrfunktion von \(\textcolor{#cc071e}{f_k}\) für \(k \in \;\textcolor{#e9b509}{]-2};+\infty[\) keinen gemeinsamen Punkt.


