Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2014 Prüfungsteil A Analysis 1
- Details
- Kategorie: Analysis 1
Bestimmen Sie die Nullstellen der Funktion \(a \, \colon x \mapsto \left( e^x - 2 \right) \cdot \left( x^3 - 2x \right)\) mit Definitionsbereich \(\mathbb R\).
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(\displaystyle b\,\colon x \mapsto \frac{\ln x}{x - 2}\) mit maximalem Definitionsbereich \(D\).
Geben Sie \(D\) an und bestimmen Sie die Gleichung der Tangente an den Graphen von \(b\) im Punkt \(\big(1|b(1)\big)\).
(6 BE)
- Details
- Kategorie: Analysis 1
Geben Sie den Term einer gebrochen-rationalen Funktion \(c\) an, die die beiden folgenden Bedingungen erfüllt:
- Der Graph von \(c\) berührt die \(x\)-Achse an der Stelle \(x = 1\);
- die Funktion \(c\) hat die Polstelle \(x = 3\).
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R^+\) definierte Funktion \(\displaystyle d\,\colon x \mapsto \frac{1}{\sqrt{x}}\). Bestimmen Sie den Term derjenigen Stammfunktion von \(d\), deren Graph durch den Punkt \((4|-1)\) verläuft.
(3 BE)
- Details
- Kategorie: Analysis 1
Betrachtet werden die folgenden Funktionsterme mit \(r,s \in \mathbb N\):
\(e(x) = \sqrt{x - r} \qquad \qquad \\ \)\(f(x) = \ln x \qquad \qquad \\ \)\(\displaystyle g(x) = -\frac{1}{x} + s\)
Jeder der Terme beschreibt genau einen der folgenden Funktionsgraphen I,II und III. Ordnen Sie die Terme den Graphen zu und geben Sie die Werte der Parameter \(r\) und \(s\) an; begründen Sie jeweils Ihre Antwort.
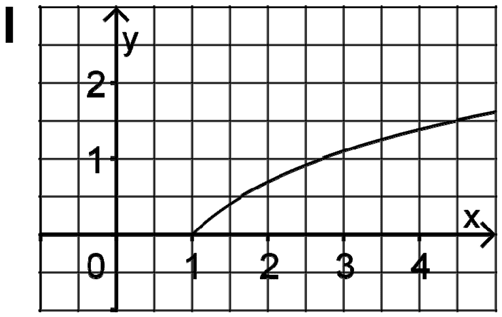
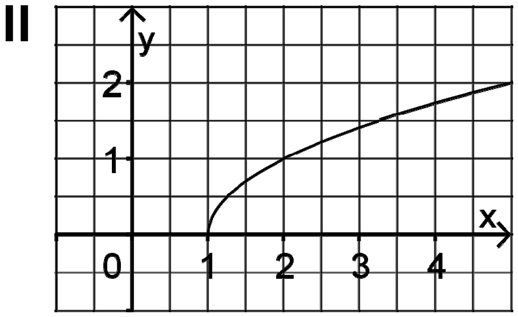
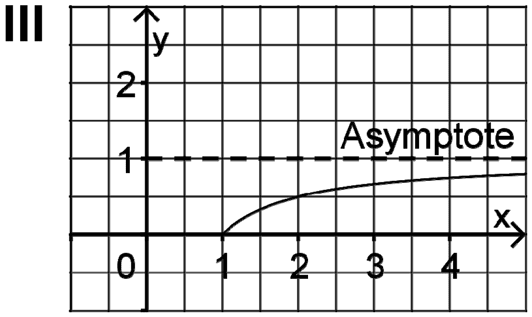
(5 BE)


