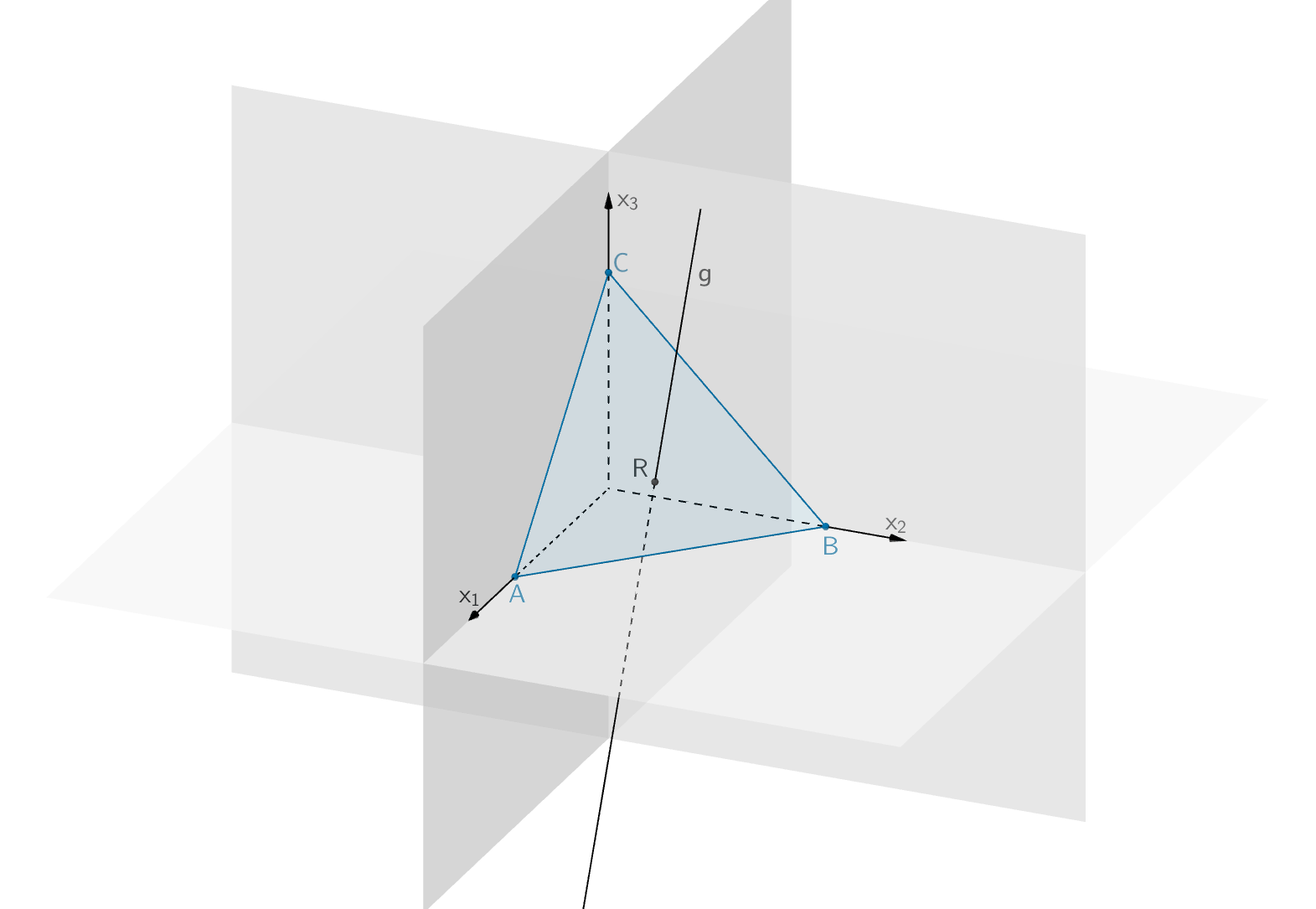
Das Dreieck \(ABC\) stellt modellhaft einen Spiegel dar. Der Punkt \(P\,(2|2|3)\) gibt im Modell die Position einer Lichtquelle an, von der ein Lichtstrahl ausgeht.
Die Richtung dieses Lichtstrahls wird im Modell durch den Vektor \(\displaystyle \overrightarrow{v} = \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix}\) beschrieben.
Geben Sie eine Gleichung der Geraden \(g\) an, entlang derer der Lichtstrahl im Modell verläuft. Bestimmen Sie die Koordinaten des Punkts \(R\), in dem \(g\) die Ebene \(E\) schneidet, und begründen Sie, dass der Lichtstrahl auf dem dreieckigen Spiegel auftrifft.
(zur Kontrolle: \(R\,(1{,}5|1{,}5|1)\))
(5 BE)
Lösung zu Teilaufgabe b
Gleichung der Geraden \(g\)
\[P\,(2|2|3)\,, \quad \overrightarrow{v} = \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix}\]
\[\begin{align*} g\,\colon\, \overrightarrow{X} &= \overrightarrow{P} + \lambda \cdot \overrightarrow{v} \\[0.8em] \overrightarrow{X} &= \begin{pmatrix} 2 \\ 2 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} \end{align*}\]
Koordinaten des Punktes \(R\) in dem \(g\) die Ebene \(E\) schneidet
\[ g\,\colon\, \overrightarrow{X} = \begin{pmatrix} 2 \\ 2 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix}\]
\[E\,\colon\, x_{1} + x_{2} + x_{3} = 4\]
Zur Berechnung der Koordinaten des Schnittpunkts \(R\), setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(g\) in die Normalengleichung der Ebene \(E\) ein, und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[\begin{align*} g \cap E\,\colon\, 2 - \lambda + 2 - \lambda + 3 - 4\lambda &= 4 \\[0.8em] 7 - 6\lambda &= 4 & &| - 7 \\[0.8em] -6\lambda &= -3 & &| : (-6) \\[0.8em] \lambda &= \frac{1}{2} \end{align*}\]
Parameterwert \(\displaystyle \lambda = \frac{1}{2}\) in die Geradengleichung von \(g\) einsetzen:
\[R \in g\,\colon\, \overrightarrow{R} = \begin{pmatrix} 2 \\ 2 \\ 3 \end{pmatrix} + \frac{1}{2} \cdot \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad R\,(1{,}5|1{,}5|1)\]
Begründung, dass der Lichtstrahl auf dem dreieckigen Spiegel auftrifft
1. Lösungsansatz: Lage des Dreiecks \(ABC\) und des Schnittpunktes \(R\)
Die Punkte \(A\), \(B\) und \(C\) liegen auf der positiven \(x_{1}\)-, \(x_{2}\)- bzw. \(x_{3}\)-Achse. Sie sind die Spurpunkte der Ebene \(E\), d.h. die Schnittpunkte der Ebene \(E\) mit den Koordinatenachsen. Das Dreieck \(ABC\), welches modellhaft den Spiegel darstellt, repräsentiert demnach den Teil der Ebene \(E\), der im I. Oktanten liegt. Der Schnittpunkt \(R\) der Geraden \(g\) (Lichtstrahl) und der Ebene \(E\) liegt ebenfalls im I. Oktanten. Folglich trifft der Lichtstrahl auf dem dreieckigen Spiegel auf.
2. Lösungsansatz: vektorielle Begründung
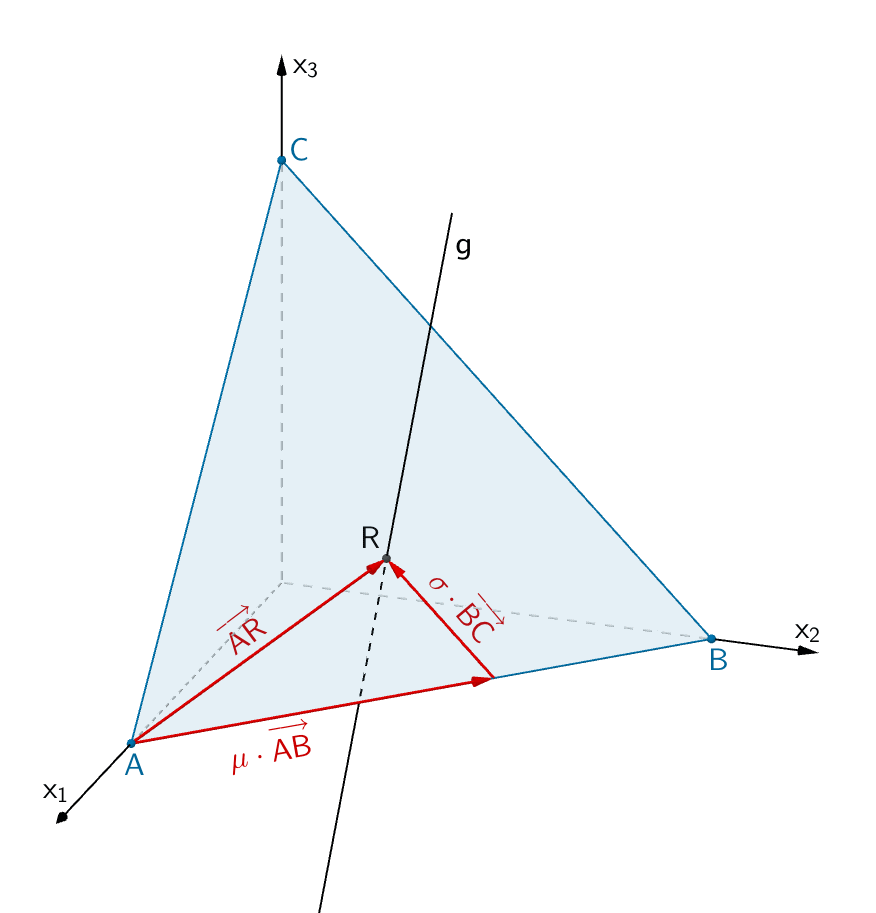
Wählt man als Bezugspunkt z.B. Punkt \(A\) des Dreiecks \(ABC\), so kann die relative Lage eines beliebigen Punktes innerhalb des Dreiecks \(ABC\) durch eine Vektoraddition, wie beispielsweise \( \mu \cdot \overrightarrow{AB} + \sigma \cdot \overrightarrow{BC}\,;\) \(\mu,\sigma \in \;]0;1[\,\), beschrieben werden.
Liegt der Schnittpunkt \(R\) innerhalb des Dreiecks, muss die Vektorgleichung \(\overrightarrow{AR} = \mu \cdot \overrightarrow{AB} + \sigma \cdot \overrightarrow{BC}\) eine eindeutige Lösung besitzen.
\[A\,(4|0|0)\,,\enspace B\,(0|4|0)\,, \enspace C\,(0|0|4)\,,\enspace R\,(1{,}5|1{,}5|1)\]
\[\begin{align*}\overrightarrow{AR} &= \mu \cdot \overrightarrow{AB} + \sigma \cdot \overrightarrow{BC} \\[0.8em] \overrightarrow{R} - \overrightarrow{A} &= \mu \cdot (\overrightarrow{B} - \overrightarrow{A}) + \sigma \cdot (\overrightarrow{C} - \overrightarrow{B}) \\[0.8em] \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 1 \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} &= \mu \cdot \left[ \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \right] + \sigma \cdot \left[ \begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} \right] \\[0.8em] \begin{pmatrix} -2{,}5 \\ 1{,}5 \\ 1 \end{pmatrix} &= \mu \cdot \begin{pmatrix} -4 \\ 4 \\ 0 \end{pmatrix} + \sigma \cdot \begin{pmatrix} 0 \\ -4 \\ 4 \end{pmatrix} \end{align*}\]
Lineares Gleichungssystem lösen:
\[\begin{align*} \text{I} & & & & -2{,}5 &= -4\mu & & \Longrightarrow \quad \mu = \frac{-2{,}5}{-4} = \frac{5}{8} \\[0.8em] \text{II} & & & \wedge & 1{,}5 &= 4\mu - 4\sigma \\[0.8em] \text{III} & & & \wedge & 1 &= 4\sigma & & \Longrightarrow \quad \sigma = \frac{1}{4} \end{align*}\]
\[\begin{align*}\mu = \frac{5}{8}\,; \enspace \sigma = \frac{1}{2} \; \text{in II}\,\colon \enspace 1{,}5 &= 4 \cdot \frac{5}{8} - 4 \cdot \frac{1}{4} \\[0.8em] 1{,}5 &= \frac{5}{2} - 1 \\[0.8em] 1{,}5 &= 1{,}5 \quad (\text{w}) \end{align*}\]
Die Gleichung \(\overrightarrow{AR} = \mu \cdot \overrightarrow{AB} + \sigma \cdot \overrightarrow{BC}\,;\) \(\mu,\sigma \in \;]0;1[\) besitzt mit \(\displaystyle \mu = \frac{5}{8}\) und \(\displaystyle \sigma = \frac{1}{4}\) eine eindeutige Lösung. Folglich liegt der Punkt \(R\) innerhalb des Dreiecks \(ABC\) und der Lichtstrahl trifft auf den Spiegel auf.