Berechnen Sie, welche Menge der Flüssigkeit verkauft werden muss, damit das Unternehmen den größten Gewinn erzielt.
(5 BE)
Lösung zu Teilaufgabe 2d
Die notwendige Bedingung für maximalen Gewinn lautet:
\[G'(x) = 0\]
Gewinnfunktion \(G\) beschreiben:
\[\begin{align*}G(x) &= E(x) - K(x) \\[0.8em] &= 23x - (x^{3} - 12x^{2} + 50x + 20) \\[0.8em] &=-x^{3} + 12x^{2} - 27x - 20 \end{align*}\]
Im Sachzusammenhang ist der in Teilaufgabe 2c ermittelte Bereich \(4 < x < 8{,}6\) ein sinnvoller Definitionsbereich der Gewinnfunktion \(G\).
\(G(x) = -x^{3} + 12x^{2} - 27x - 20; \; D_{G} = ]4;8{,}6[\)
Erste Ableitung \(G'\) bilden:
Hierfür wird die Ableitung einer Potenzfunktion sowie die Summen- und die Faktorregel benötigt.
\[G(x) = -x^{3} + 12x^{2} - 27x - 20\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*}G'(x) &= -3x^{2} + 12 \cdot 2x - 27 \\[0.8em] &= -3x^{2} + 24x - 27 \end{align*}\]
Nullstelle von \(G'\) ermitteln:
\[\begin{align*}G'(x) &= 0 \\[0.8em] -3x^{2} + 24x - 27 &= 0 \end{align*}\]
Mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel) folgt:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{-24 \pm \sqrt{24^{2} - 4 \cdot (-3) \cdot (-27)}}{2 \cdot (-3)} \\[0.8em] &= 4 \pm \sqrt{7} \end{align*}\]
\[x_{1} = 4 + \sqrt{7} \approx 6{,}6 \; \wedge \; (x_{2} = 4 - \sqrt{7} \approx 1{,}4)\]
Mit \(x \in \; ]4;8{,}6[\) ist \(x = 6{,}6\) eine im Sachzusammenhang sinnvolle Lösung der quadratischen Gleichung.
Nachweis, dass \(G\) an der Stelle \(x \approx 6{,}6\) ein relatives Maximum hat:
Da \(G''(x)\) einfach zu bilden ist, wird das Vorzeichen von \(G''(6{,}6)\) betrachtet.
Zweite Ableitung \(G''\) bilden:
\[G'(x) = -3x^{2} + 24x - 27\]
\[G''(x) = -6x + 24\]
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\[G''(6{,}6) = -6 \cdot 6{,}6 + 24 = -15{,}6 \quad \Longrightarrow \quad G''(6{,}6) < 0\]
Also ist \(G(6{,}6)\) ein relatives Maximum der Gewinnfunktion \(G\).
Betrachtung möglicher Randmaxima:
Mit dem Definitionsbereich \(D_{G} = \;]4;8{,}6[\) ist die Gewinnfunktion \(G\) für \(x = 4\) und \(x = 8{,}6\) nicht definiert. Also kann es keine Randmaxima geben. Diese Erkenntnis vermittelt auch die Zeichnung zu Teilaufgabe 2c.
Schlussfolgerung:
Um den größten Gewinn zu erzielen, muss das Unternehmen ca. 6,6 Kubikmeter der Flüssigkeit verkaufen.
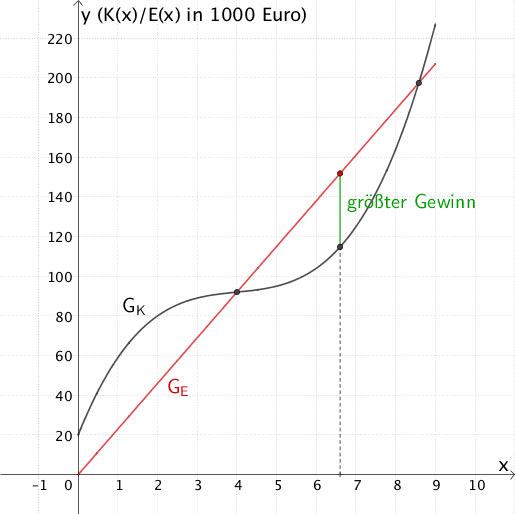
Veranschaulichung: Größter Gewinn \(G(6{,}6)\)


