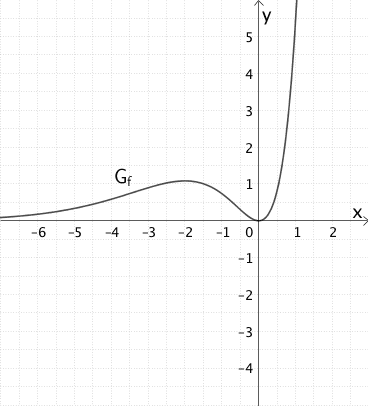
Die Abbildungen zeigen den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten und stetigen Funktion \(f\) sowie die Graphen A, B und C.
Entscheiden Sie, welcher der Graphen A, B oder C den Graphen der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t) dt\) darstellt, indem Sie begründen weshalb die beiden anderen Graphen nicht in Frage kommen.
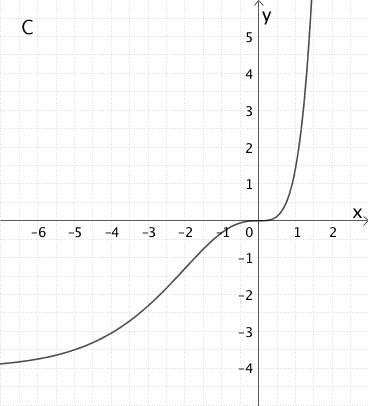
Graph C zeigt den Graphen der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t) dt\).
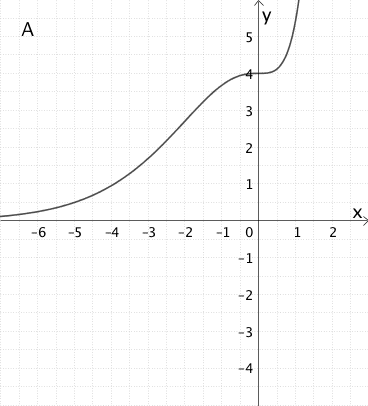
Begründung, weshalb Graph A nicht in Frage kommt

Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Die Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t) dt\) besitzt an der unteren Integrationsgrenze \(x = 0\) eine Nullstelle, d. h. es gilt: \(I_{0}(0) = 0\) und der Graph \(G_{I_{0}}\) der Integralfunktion \(I_{0}\) verläuft durch den Koordinatenursprung \((0|0)\).
Graph A verläuft eindeutig nicht durch den Koordinatenursprung und stellt somit nicht den Graphen der Integralfunktion \(I_{0}\) dar.
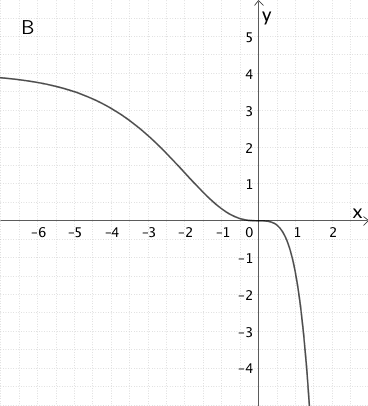
Begründung, weshalb Graph B nicht in Frage kommt

Dem Verlauf des Graphen \(G_{f}\) ist zu entnehmen, dass im abgebildeten Bereich \(f(x) \geq 0\) gilt.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung ist die Integralfunktion \(I_{0}\) eine Stammfunktion der Funktion \(f\) und es gilt \(I'_{0}(x) = f(x)\).
\[\Longrightarrow \quad I'_{0}(x) \geq 0\]
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Gemäß dem Monotoniekriterium ist der Graph \(G_{I_{0}}\) der Integralfunktion \(I_{0}\) also im abgebildeten Bereich monoton steigend.

Graph B ist im abgebildeten Bereich monoton fallend und stellt deshalb nicht den Graphen der Integralfunktion \(I_{0}\) dar.
Nach dem Ausschlussprinzip ist Graph C der Graph der Integralfunktion \(I_{0}\).
Nachfolgende Erläuterung ist im Sinne der Aufgabenstellung nicht erforderlich. Sie dient lediglich dem besseren Verständnis.

Graph \(C\) verläuft durch den Koordinatenursprung und ist im abgebildeten Bereich monoton steigend.
Da \(G_{f}\) die \(x\)-Achse im Koordinatenursprung berührt (vgl. oben), ist \(x = 0\) doppelte Nullstelle von \(f\) (ohne Vorzeichenwechsel). Mit \(I'_{0}(0) = f(0) = 0\) und \(I'_{0}(x) \geq 0\) folgt, dass der Graph der Integralfunktion \(I_{0}\) an der Stelle \(x = 0\) eine waagrechte Tangente hat und in der Umgebung von \(x = 0\) streng monoton steigt. Das bedeutet, dass \(G_{I_{0}}\) an der Stelle \(x = 0\) einen Terrassenpunkt hat. Graph C bestätigt dies.

