An der Stelle \(x = 2\) hat \(G_{f}\) einen Wendepunkt. Beschreiben Sie, wie man rechnerisch vorgehen könnte, um dies zu begründen. Geben Sie die Bedeutung der \(x\)-Koordinate des Wendepunkts im Sachzusammenhang an.
(3 BE)
Lösung zu Teilaufgabe f
Vorgehensweise für die rechnerische Begründung des Wendepunkts
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
1) \(f''(2) = 0\) nachweisen
2) Vorzeichenwechsel von \(f''\) an der Stelle \(x = 2\) nachweisen (z.B. mit einer Kümmungstabelle)
Bedeutung der \(x\)-Koordinate des Wendepunkts im Sachzusammenhang
Anmerkung:
An einer Wendestelle ist die lokale/momentane Änderungsrate einer Funktion/einer Größe extremal (größte Zu- oder Abnahme).
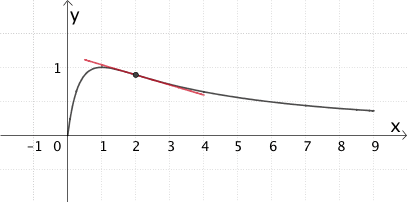
Zwei Stunden \((x = 2)\) nach Einnahme der Tablette ist die Abnahme der Wirkstoffkonzentration am größten (Skizze nicht verlangt).


