Um sicherzustellen, dass jeweils genau 50 Gummibärchen in eine Tüte gelangen, fallen diese einzeln nacheinander aus einer Öffnung des Behälters in den Verpackungsautomaten. Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit mit dem folgenden Term berechnet werden kann:
\[\sum \limits_{k\,=\,0}^{3}(0{,}75^{k} \cdot 0{,}25)\]
(2 BE)
Lösung zu Teilaufgabe 2b
Mögliche Beschreibungen des Ereignisses
„Unter den ersten vier Gummibärchen, die in die Tüte gelangen, ist mindestens ein rotes Gummibärchen."
oder
„Spätestens das vierte Gummibärchen, das in die Tüte gelangt, ist ein rotes Gummibärchen."
Ausführliche Erklärung (nicht verlangt)
\(\textcolor{#cc071e}{p = 0{,}25}\) (Anteil roter Gummibärchen, vgl. Angabe Aufgabe 2)
\(q = 1 - p = 0{,}75\) (Anteil andersfarbiger Gummibärchen)
\[\begin{align*}\sum \limits_{k\,=\,0}^{3}(0{,}75^{k} \cdot 0{,}25)\enspace &= \enspace \;\, \underbrace{0{,}75^{0} \cdot\textcolor{#cc071e}{0{,}25}}_{\textcolor{#cc071e}{r}} &&\text{„Das}\,\textcolor{#cc071e}{\text{erste}}\,\text{ist ein}\,\textcolor{#cc071e}{\text{rotes Gummibärchen.}}" \\[0.8em] &\quad+ \underbrace{0{,}75^{1} \cdot \textcolor{#cc071e}{0{,}25}}_{\overline{r}\,\textcolor{#cc071e}{r}}&&\text{„Erst das}\,\textcolor{#cc071e}{\text{zweite}}\,\text{ist ein}\,\textcolor{#cc071e}{\text{rotes Gummibärchen.}}"\\[0.8em] &\quad+ \underbrace{0{,}75^{2} \cdot \textcolor{#cc071e}{0{,}25}}_{\overline{r}\,\overline{r}\,\textcolor{#cc071e}{r}}&&\text{„Erst das}\,\textcolor{#cc071e}{\text{dritte}}\,\text{ist ein}\,\textcolor{#cc071e}{\text{rotes Gummibärchen.}}"\\[0.8em] &\quad+ \underbrace{0{,}75^{3} \cdot \textcolor{#cc071e}{0{,}25}}_{\overline{r}\,\overline{r}\,\overline{r}\,\textcolor{#cc071e}{r}}&&\text{„Erst das}\,\textcolor{#cc071e}{\text{vierte}}\,\text{ist ein}\,\textcolor{#cc071e}{\text{rotes Gummibärchen.}}"\end{align*}\]
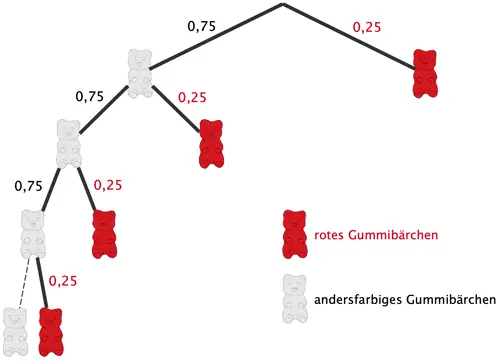
Baumdiagramm der Pfade, die der Term \(\sum \limits_{k\,=\,0}^{3}(0{,}75^{k} \cdot 0{,}25)\) eindeutig festlegt.
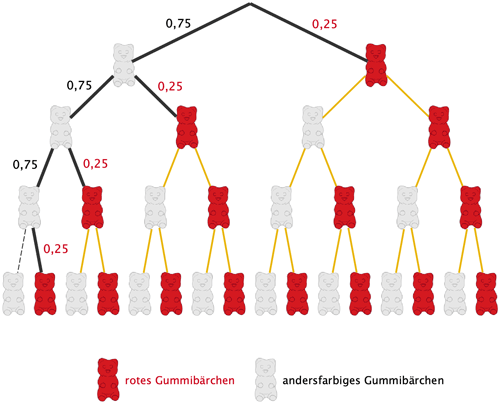
Nun sagt der Summand \(0{,}75^{k} \cdot 0{,}25\) aber nichts darüber aus, ob jeweils nach einem ersten roten Gummibärchen ein weiteres rotes oder ein andersfarbiges Gummibärchen in den Verpackungsautomaten fällt. Beides ist möglich und alle diese Möglichkeiten sind zu berücksichtigen. Einzig die Möglichkeit vier aufeinanderfolgender nicht roter Gummibärchen ist ausgeschlossen. Unter den ersten vier Gummibärchen, die in die Tüte gelangen, ist also mindestens ein rotes Gummibärchen.
Mögliche Beschreibungen des Ereignisses
„Unter den ersten vier Gummibärchen, die in die Tüte gelangen, ist mindestens ein rotes Gummibärchen."
oder
„Spätestens das vierte Gummibärchen, das in die Tüte gelangt, ist ein rotes Gummibärchen."
Anmerkung:
Die Formulierung „Unter den ersten vier Gummibärchen, die in die Tüte gelangen, ist mindestens ein rotes Gummibärchen." macht deutlich, dass sich die Wahrscheinlichkeit für dieses Ereignis auch mit der Binomialverteilung bestimmen lässt.
Das heißt, es gilt:
\[P_{0{,}25}^{4}(X \geq 1) = \sum \limits_{k\,=\,0}^{3}0{,}75^{k}\cdot 0{,}25\]
\(n = 4\) (Länge der Bernoulli-Kette)
\(\textcolor{#cc071e}{p = 0{,}25}\) (Trefferwahrscheinlichkeit für das Ereignis „Ein rotes Gummibärchen gelangt in die Tüte")
\(X\): Anzahl der roten Gummibärchen, die in die Tüte gelangen.
Die Zufallsgröße \(X\) ist nach \(B(4;0{,}25)\) binomialverteilt.
\[\begin{align*}P_{\textcolor{#cc071e}{0{,}25}}^{4}(X \geq 1) &= 1 - P_{\textcolor{#cc071e}{0{,}25}}^{4}(X = 0) \\[0.8em] &= 1 - B(4;0{,}25;0) &&|\;\text{Stochastisches Tafelwerk (ST)}\\[0.8em] &\overset{\text{ST}}{=} 1 - 0{,}31641 \\[0.8em] &\approx 0{,}68359 \approx 68{,}4\,\%\end{align*}\]
\[\begin{align*}\sum \limits_{k\,=\,0}^{3}(0{,}75^{k} \cdot 0{,}25) &= 0{,}75^{0} \cdot 0{,}25 + 0{,}75^{1} \cdot 0{,}25 + 0{,}75^{2} \cdot 0{,}25 + 0{,}75^{3} \cdot 0{,}25 \\[0.8em] &\approx 0{,}68359 \approx 68{,}4\,\%\end{align*}\]
Bildnachweis (Montage): Amberrose Nelson auf Pixabay


