Die binomialverteilte Zufallsgröße \(Y\) hat die Parameter \(n = 8\) und \(p_Y = 1 - p_X\). Kennzeichnen Sie in Abbildung 2 eine Fläche, die die Wahrscheinlichkeit \(P(Y \geq 6)\) darstellt.
(2 BE)
Lösung zu Teilaufgabe 3b
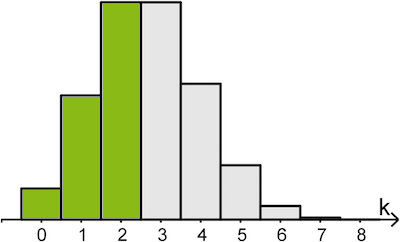
Ausführliche Erklärung (nicht verlangt)
Die binomialverteilte Zufallsgröße \(X\) hat die Parameter \(\textcolor{#0087c1}{n = 8}\) und \(\textcolor{#cc071e}{p_X = \dfrac{1}{3}}\) (vgl. Teilaufgabe 3a)
Die binomialverteilte Zufallsgröße \(Y\) hat die Parameter \(\textcolor{#0087c1}{n = 8}\) und \(\textcolor{#cc071e}{p_Y} = 1 - p_X = 1 - \dfrac{1}{3} = \textcolor{#cc071e}{\dfrac{2}{3}}\).
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
\(p_X\) ist die Wahrscheinlichkeit für einen Treffer der Zufallsgröße \(X\); \(1 - p_X\) ist die Wahrscheinlichkeit für eine Niete (Nicht-Treffer) der Zufallsgröße \(X\).
Bei gleicher Länge der Bernoullikette \(\textcolor{#0087c1}{n = 8}\) beschreibt die Zufallsgröße \(Y\) mit \(p_Y = 1 - p_X\) somit die Anzahl der Nieten der Zufallsgröße \(X\).
\(Y \geq 6\) bedeutet dann bezüglich der Zufallsgröße \(X\) „mindestens sechs Nieten" und als Treffer formuliert „höchstens zwei Treffer", sodass gilt:
\[P_{\textcolor{#cc071e}{\frac{2}{3}}}^{\textcolor{#0087c1}{8}}(Y \geq 6) = P_{\textcolor{#cc071e}{\frac{1}{3}}}^{\textcolor{#0087c1}{8}}(\textcolor{#89ba17}{X \leq 2})\]
Also sind in Abbildung 2 die Säulen entsprechend zu kennzeichnen, welche die Wahrscheinlichkeiten \(\textcolor{#89ba17}{P(X = 0)}\) \(\textcolor{#89ba17}{P(X = 1)}\) und \(\textcolor{#89ba17}{P(X = 2)}\) darstellen.



