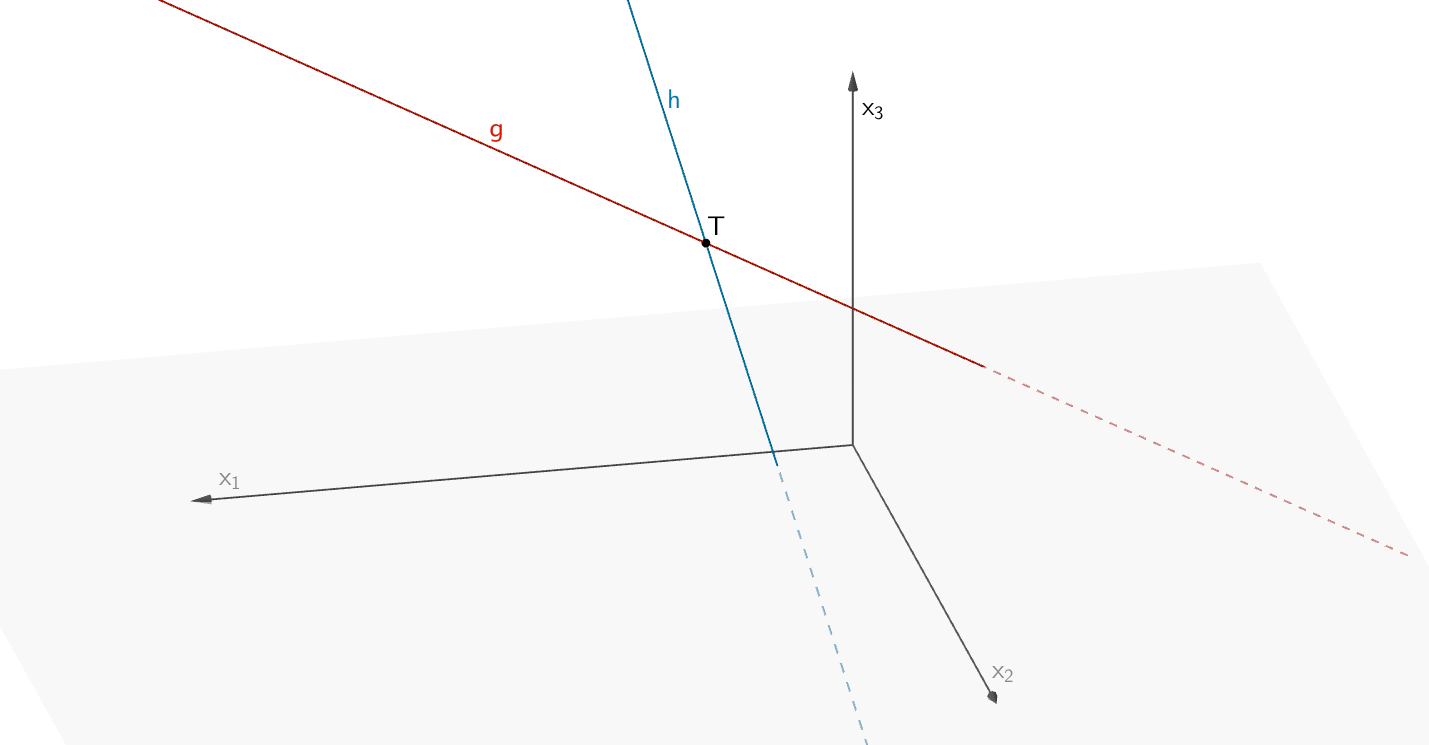
In einem kartesischen Koordinatensystem sind die Geraden \(\displaystyle g\;\colon\, \vec{X} = \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}\), \(\lambda \in \mathbb R\,\), und \(\displaystyle h\;\colon\, \vec{X} = \begin{pmatrix} -1 \\ 5 \\ -9 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -2 \\ 4 \end{pmatrix}\), \(\mu \in \mathbb R\,\), gegeben. Die Geraden \(g\) und \(h\) schneiden sich im Punkt \(T\).
Bestimmen Sie die Koordinaten von \(T\).
(Ergebnis: \(T\,(2|-1|3)\))
(4 BE)
Lösung zu Teilaufgabe 2a
\[g\,\colon\; \overrightarrow{X} = \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix}\,; \enspace \lambda \in \mathbb R\]
\[h\,\colon\; \overrightarrow{X} = \begin{pmatrix} -1 \\ 5 \\ -9 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -2 \\ 4 \end{pmatrix}\,; \enspace \mu \in \mathbb R\]
Lagebeziehung von Geraden
| \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}; \; \lambda \in \mathbb R \enspace\) und \(\enspace h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R\) | |||
| \(\overrightarrow{u} = k \cdot \overrightarrow{v}, \; k \in \mathbb R \\[0.8em] \Longrightarrow \enspace \overrightarrow{u} \parallel \overrightarrow{v}\) | \(\overrightarrow{u} \neq k \cdot \overrightarrow{v}, \; k \in \mathbb R \\[0.8em] \Longrightarrow \enspace \overrightarrow{u} \nparallel \overrightarrow{v}\) | ||
|
\(A \in h\) \(\Longrightarrow \enspace\)\(g\) und \(h\) sind identisch. |
\(A \notin h\) \(\Longrightarrow \enspace\)\(g\) und \(h\) sind (echt) parallel (ggf. Abstand berechnen). |
\(\overrightarrow{A} + \lambda \cdot \overrightarrow{u} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\) - genau eine Lösung \(\Longrightarrow \enspace\)\(g\) und \(h\) schneiden sich in einem Schnittpunkt \(S\) unter dem Schnittwinkel \(\alpha\) (ggf. Schnittpunkt und/oder Schnittwinkel berechnen).
|
\(\overrightarrow{A} + \lambda \cdot \overrightarrow{u} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\) - keine Lösung \(\Longrightarrow \enspace\)\(g\) und \(h\) verlaufen windschief zueinander (ggf. Abstand berechnen).
|
Zur Berechnug des Schnittpunktes \(T\) der Geraden \(g\) und \(h\) werden die Ortsvektoren \(\overrightarrow{X}\) der Geradengleichungen von \(g\) und \(h\) gleichgesetzt. Es ergibt sich ein überbestimmtes lineares Gleichungssystem mit drei Gleichungen für die zwei zu bestimmenden Parametren \(\lambda\) und \(\mu\).
\[g \cap h\,\colon\; \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -1 \\ 5 \\ -9 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -2 \\ 4 \end{pmatrix}\]
Lineares Gleichungssystem aufstellen:
\[\begin{align*} \text{I} & & & & 8 + 3\lambda &= -1 + \mu \\[0.8em] \text{II} & & \wedge & & 1 + \lambda &= 5 - 2\mu \\[0.8em] \text{III} & & \wedge & & 7 + 2\lambda &= -9 + 4\mu \\[2.4em] 2 \cdot \text{I} + \text{II}\,\colon\; & & & & 17 + 7\lambda &= 3 & &| - 17 \\[0.8em] & & & & 7\lambda &= -14 & &| : 7 \\[0.8em] & & & & \lambda &= -2 \\[2.4em] \lambda = -2 \; \text{in I}\,\colon\; & & & & 8 + 3 \cdot (-2) &= -1 + \mu & &| + 1 \\[0.8em] & & & & 8 - 6 + 1 &= \mu \\[0.8em] & & & & 3 &= \mu \\[2.4em] \lambda = -2\,; \enspace \mu = 3 \; \text{in III}\,\colon\; & & & & 7 + 2 \cdot (-2) &= -9 + 4 \cdot 3 \\[0.8em] & & & & 3 &= 3 \enspace (\text{w}) \end{align*}\]
\(\Longrightarrow \quad \lambda = -2\) und \(\mu = 3\) ist eindeutige Lösung
Parameterwert \(\lambda = -2\) in die Geradengleichung von \(g\) oder Parametrewert \(\mu = 3\) in die Geradengleichung von \(h\) einsetzen:
\[T \in g\,\colon\; \overrightarrow{T} = \begin{pmatrix} 8 \\ 1 \\ 7 \end{pmatrix} - 2 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \]
\[\Longrightarrow \quad T\,(2|-1|3)\]
\[T \in h\,\colon\; \overrightarrow{T} = \begin{pmatrix} -1 \\ 5 \\ -9 \end{pmatrix} + 3 \cdot \begin{pmatrix} 1 \\ -2 \\ 4 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \]
\[\Longrightarrow \quad T\,(2|-1|3)\]
Schnittpunkt \(T\) der Geraden \(g\) und \(h\)