Ein geschlossenes Zelt, das auf horizontalem Untergrund steht, hat die Form einer Pyramide mit quadratischer Grundfläche. Die von der Zeltspitze ausgehenden Seitenkanten werden durch vier gleich lange Stangen gebildet. das Zelt ist 6 m hoch, die Seitenlänge des Zeltbodens beträgt 5 m.
Das Zelt wird in einem kartesischen Koordinatensystem (vgl. Abbildung) modellhaft durch eine Pyramide \(ABCDS\) mit der Spitze \(S(2{,}5|2{,}5|6)\) dargestellt. Der Punkt \(A\) liegt im Koordinatenursprung, \(C\) hat die Koordinaten \((5|5|0)\). Der Punkt \(B\) liegt auf der \(x_{1}\)-Achse, \(D\) auf der \(x_{2}\)-Achs. Das Dreieck \(CDS\) liegt in der Ebene \(E\colon 12x_{2} + 5x_{3} = 60\). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Geben Sie die Koordinaten der Punkte \(B\) und \(D\) an und zeichnen Sie die Pyramide in ein Koordinatensystem ein.
(3 BE)
Lösung zu Teilaufgabe a
Räumliches Objekt im dreidimensionalen kartesischen Koordinatensystem zeichnen
Koordinaten der Punkte \(B\) und \(D\)
Anmerkung:
Die Koordinaten der Punkte \(B\) und \(D\) sind lediglich anzugeben. Jede Erklärung kann entfallen.
Die Pyramide \(ABCDS\) hat die quadratische Grundfläche \(ABCD\) mit der Seitenlänge 5 LE (Längeneinheiten). Die Benennung der Eckpunkte des Quadrats erfolgt gegen den Uhrzeigersinn.
Anhand der Koordinaten der Punkte \(A(0|0|0)\) und \(C(5|5|0)\) ergeben sich die Koordinaten der Punkte \(B\) und \(D\) zu:
\(B(5|0|0)\), \(D(0|5|0)\).
Zeichnung der Pyramide \(ABCDS\)
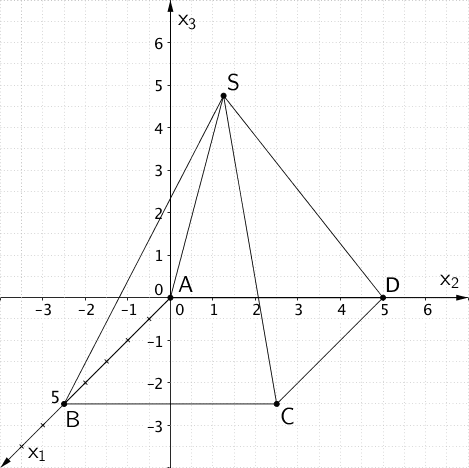
Zeichnung der Pyramide \(ABCDS\) mit der quadratischen Grundfläche \(ABCD\)


