Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral \(\displaystyle \int_{-2}^2 f(x)dx\).
(3 BE)
Lösung zu Teilaufgabe 1e
Der Wert des bestimmten Integrals \(\displaystyle \int_{-2}^2 f(x)dx\) entspricht der Flächenbilanz des Inhalts der Fläche, die \(G\) und die \(x\)-Achse im Bereich \(-2 \leq x \leq 2\) einschließen. Da die Fläche vollständig unterhalb der \(x\)-Achse liegt, zählt ihr Inhalt negativ.
1. Möglichkeit: „Kästchen zählen"
Der Flächeninhalt lässt sich durch ca. 16 Kästchen zu je 0,25 FE annähern.
\[16 \cdot 0{,}25 = 4\]
\[\Rightarrow\;\int_{-2}^2 f(x)dx \approx \textcolor{#cc071e}{\boldsymbol{–}}\,4\]

2. Möglichkeit: Annäherung durch ein Trapez
Das Trapez wird so gewählt, dass überstehende Flächenanteile in etwa unberücksichtigte Flächenanteile ausgleichen.
Flächeninhalt eines Trapezes
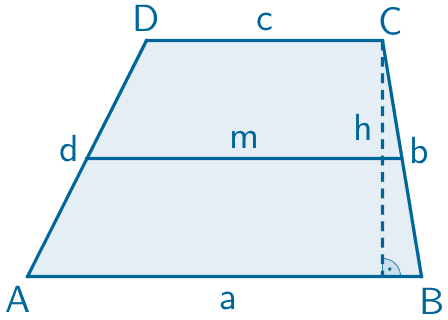
\[A = m \cdot h = \frac{a + c}{2} \cdot h\]
\[\int_{-2}^2 f(x)dx \approx \textcolor{#cc071e}{–}\,\frac{\textcolor{#cc071e}{1}+ \textcolor{#cc071e}{4}}{2} \cdot \textcolor{#cc071e}{1{,}5} = \textcolor{#cc071e}{–}\;3{,}75\]



