Geben Sie einen Term einer in \(\mathbb R\) definierten Funktion \(g\) an, die den Wertebereich \([-2;4]\) hat.
(2 BE)
Lösung zu Teilaufgabe 4a
zum Beispiel: \(g(x) = 3 \cdot \sin{x} + 1\) oder \(g(x) = 3 \cdot \cos{x} +1\)
Ausführliche Erklärung (nicht verlangt)
Der vorgegebene Wertebereich \([-2;4]\) schließt die Grenzen \(-2\) und \(4\) ein. Zudem soll die Funktion in \(\mathbb R\) definiert sein. Einen solchen endlichen, geschlossenen Wertebereich besitzt vor allem die in \(\mathbb R\) definierte allgemeine Sinusfunktion \(x \mapsto a \cdot \sin{\left(b(x+c)\right)}+d\) bzw. allgemeine Kosinusfunktion \(x \mapsto a \cdot \cos{\left(b(x+c)\right)} + d\).
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin\left(b(x + c)\right) + d\]
Allgemeine Kosinusfunktion
\[f(x) = a \cdot \cos\left(b(x + c)\right) + d\]
\[a,b,c,d \in \mathbb R; \enspace a,b \neq 0\]
Definitionsbereich: \(D = \mathbb R\)
Wertebereich: \(W = [-a;a]\) für \(d = 0\) und \(W= [d-a;d+a]\) für \(d \neq 0\)
Streckung mit \(a\) in \(y\)-Richtung
Streckung mit \( \dfrac{1}{b}\) in \(x\)-Richtung, Periode: \(p = \dfrac{2\pi}{\vert b \vert}\)
Verschiebung um \( -c\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
Die Parameter \(\boldsymbol{b}\) und \(\boldsymbol{c}\) bewirken eine Streckung und Verschiebung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) bzw. der Kosinusfunktion \(x \mapsto \cos{x}\) in \(x\)-Richtung und beeinflussen den Wertebereich nicht.
Der Ansatz erfolgt deshalb unter Berücksichtigung der Parameter \(\textcolor{#cc071e}{a}\) und \(\textcolor{#0087c1}{d}\), welche eine Streckung und Verschiebung in \(y\)-Richtung bewirken.
\(g(x) = \textcolor{#cc071e}{a} \cdot \sin{x} + \textcolor{#0087c1}{d}\) bzw. \(g(x) = \textcolor{#cc071e}{a} \cdot \cos{x} + \textcolor{#0087c1}{d}\) mit Wertebereich \([\textcolor{#0087c1}{d} - \textcolor{#cc071e}{a}; \textcolor{#0087c1}{d}+\textcolor{#cc071e}{a}]\)
Da der Wertebereich \([-2;4]\) die dreifache Intervallbreite des Wertebereichs \([-1;1]\) der Sinus- bzw. Kosinusfunktion vorgibt, wird zunächst \(\textcolor{#cc071e}{a = 3}\) gewählt. Die Funktion \(x \mapsto \textcolor{#cc071e}{3} \cdot \sin{x}\) bzw. \(x \mapsto \textcolor{#cc071e}{3} \cdot \cos{x}\) hat dann den Wertebereich \([\textcolor{#cc071e}{-3};\textcolor{#cc071e}{3}]\).
\(\textcolor{#0087c1}{d = 1}\) verschiebt den Graphen von \(x \mapsto \textcolor{#cc071e}{3} \cdot \sin{x}\) bzw. \(x \mapsto \textcolor{#cc071e}{3} \cdot \cos{x}\) um \(\textcolor{#0087c1}{1}\) in positive \(y\)-Richtung.
\(g(x) = \textcolor{#cc071e}{3} \cdot \sin{x} + \textcolor{#0087c1}{1}\) bzw. \(g(x) = \textcolor{#cc071e}{3} \cdot \cos{x} + \textcolor{#0087c1}{1}\) mit Wertebereich \([\textcolor{#0087c1}{1}-\textcolor{#cc071e}{3};\textcolor{#0087c1}{1}+\textcolor{#cc071e}{3}] = [-2;4]\)
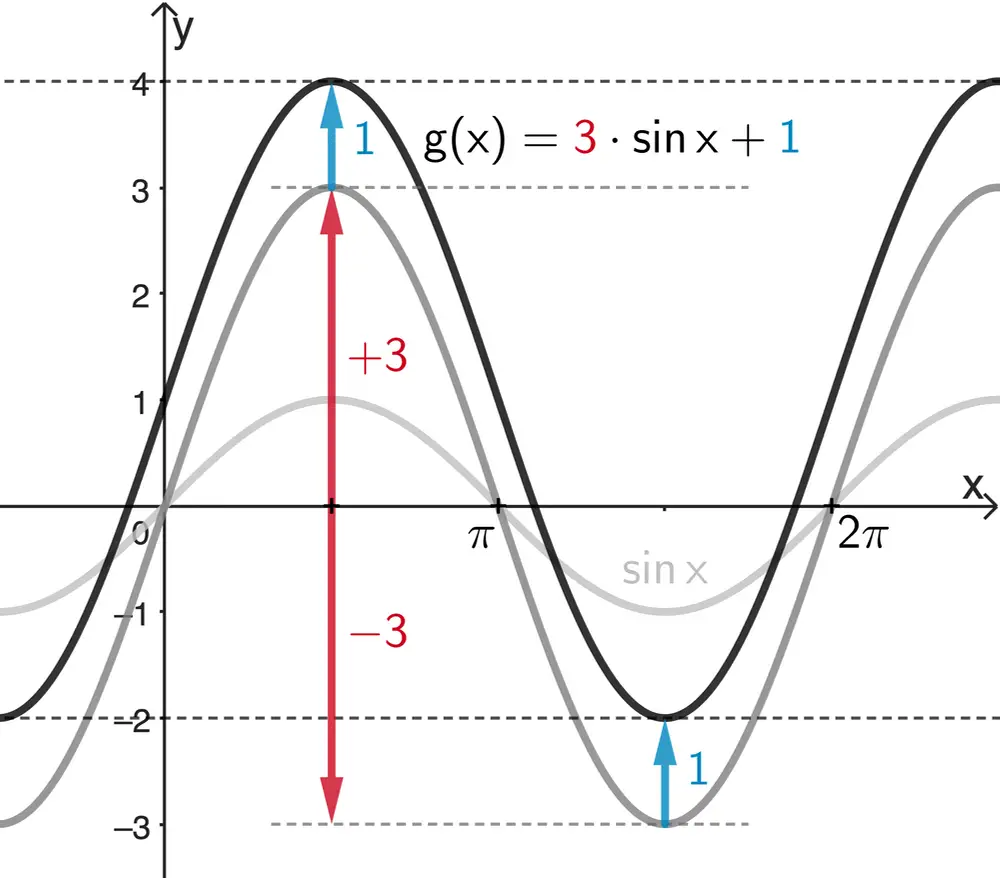
Veranschaulichung am Beispiel der Funktion \(g \colon x \mapsto 3 \cdot \sin{}x + 1\)
Anmerkung
Es kommen auch andere Funktionen in Frage wie beispielsweise die in \(\mathbb R\) definierte gebrochenrationale Funktion \(x \mapsto \dfrac{6x}{x^2+1} +1\), deren Wertebereich \([-2;4]\) durch globale Extrema festgelegt wird. Aber diese sind kompliziert zu finden.
![Graph einer in R definierten gebrochenrationalen Funktion, deren Wertebereich [-2;4] globale Extrema festlegen.](/images/stories/B2024_PT_A_A1/B2024_PT_A_A1_4a_2_web.png)


