Im Rahmen der Show müssen Aufgaben aus verschiedenen Fachgebieten gelöst werden. Die Anzahl der von einem Kandidaten zu lösenden Aufgaben aus dem Fachgebiet Mathematik ist gleich der Augensumme, die von ihm bei einmaligem Werfen zweier Würfel erzielt wird. Die beiden Würfel tragen jeweils auf zwei Seitenflächen die Augenzahl 0, auf drei Seitenflächen die Augenzahl 1 und auf einer Seitenfläche die Augenzahl 2.

Berechnen Sie die Wahrscheinlichkeit dafür, dass der erste Kandidat genau zwei Aufgaben aus dem Fachgebiet Mathematik lösen muss.

(4 BE)

Lösung zu Teilaufgabe 3a

Der geschilderte Sachverhalt nennt keine weiteren Bedingungen, die das Ergebnis beim Würfeln eines Kandidaten beeinflussen. Jeder Kandidat nimmt unter denselben Voraussetzungen am Würfeln teil. Somit spielt es keine Rolle, welcher Kandidat betrachtet wird.

Augenzahlen des Würfels:

zweimal Augenzahl 0 \(\displaystyle \quad \Longrightarrow \quad p_0 = \frac{2}{6} = \frac{1}{3}\)

dreimal Augenzahl 1 \(\displaystyle \quad \Longrightarrow \quad p_1 = \frac{3}{6} = \frac{1}{2}\)

einmal Augenzahl 2 \(\displaystyle \quad \Longrightarrow \quad p_2 = \frac{1}{6}\)

Ereignis "Augensumme ist 2" = \(\{\,02\,,\,11\,,\,20\,\}\)

Zufallsgröße \(X \colon \enspace\) Anzahl der von einem Kandidaten zu lösenden Aufgaben aus dem Fachgebiet Mathematik

Die Zufallsgröße \(X\) ordnet jedem Ergebnis des Ereignisses "Augensumme ist 2" die Zahl 2 zu.

\[\begin{align*}P(X = 2) &= P(\{\,02\,,\,11\,,\,20\,\}) \\[0.8em] &= p_0 \cdot p_2 + p_1 \cdot p_1 + p_2 \cdot p_0 \\[0.8em] &= \frac{1}{3} \cdot \frac{1}{6} + \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{6} \cdot \frac{1}{3} \\[0.8em] &= 2 \cdot \frac{1}{3} \cdot \frac{1}{6} + \left( \frac{1}{2}\right)^2 \\[0.8em] &=\frac{13}{36} \approx 0{,}361 = 36{,}1\,\% \end{align*}\]

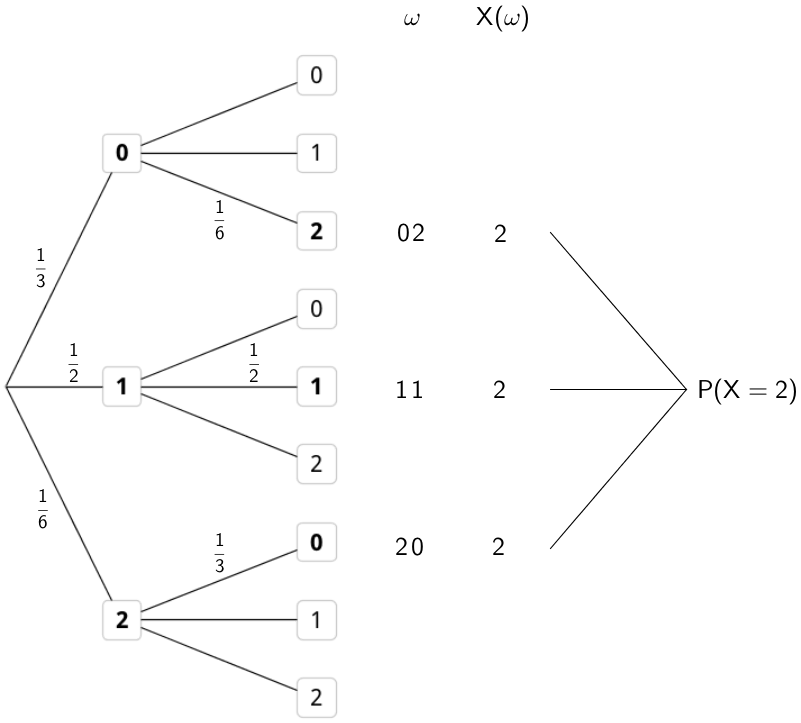
Baumdiagramm: Wahrscheinlichkeit \(\,P(X = 2)\,\) dafür, dass ein Kandidat zwei Aufgaben aus dem Fachgebiet Mathematik lösen muss