Nach der Wahl darf die Partei A in einem Ausschuss drei Sitze besetzen. Von den acht Stadträtinnen und vier Stadträten der Partei A, die Interesse an einem Sitz in diesem Ausschuss äußern, werden drei Personen per Losentscheid als Ausschussmitglieder bestimmt.
Die Zufallsgröße \(X\) beschreibt die Anzahl der weiblichen Ausschussmitglieder der Partei A. Abbildung 1 zeigt die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mit \(P(X = 0) = \frac{1}{55}\) und \(P(X = 3) = \frac{14}{55}\).
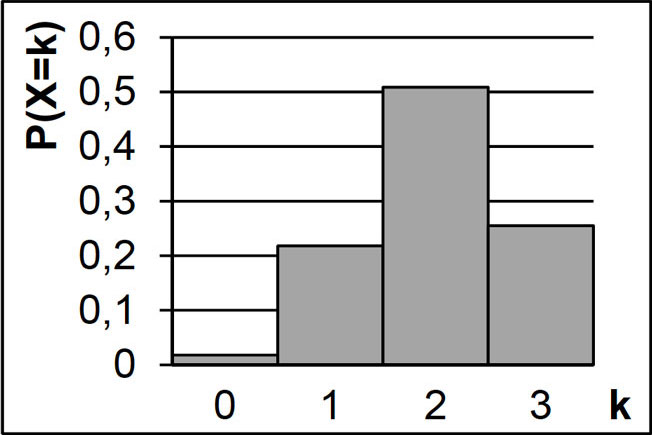Abb. 1
Abb. 2
Berechnen Sie die Wahrscheinlichkeiten \(P(X = 1)\) und \(P(X = 2)\).
(Ergebnis: \(P(X = 1) = \frac{12}{55}\), \(P(X = 2) = \frac{28}{55}\))
(4 BE)
Lösung zu Teilaufgabe 3a
Zufallsgröße \(X\,\colon\;\)Anzahl der weiblichen Ausschussmitglieder der Partei A
1. Lösungsansatz: Urnenmodel Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge
Die Stadträtinnen und Stadträte der Partei A ziehen nacheinander je ein Los. Die Vergabe der Lose erfolgt einmalig (ohne Zurücklegen). Wer welches Los zieht spielt keine Rolle (ohne Reihenfolge). Entscheidend ist nur, dass die Partei A drei Sitze im Ausschuss besetzen darf.
Urnenmodell: „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge"
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
(vgl. Merkhilfe)
- 8 Stadträtinnen
- 4 Stadträte
- 3 Sitze im Ausschuss für die Partei A
Binomialkoeffizient
Der Binomialkoeffizient gibt an, wie viele Möglichkeiten es gibt, aus einer Menge mit \(n\) Elementen eine Teilmenge mit \(k\) Elementen zu bilden.
\[\binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} = \frac{n \cdot (n - 1) \cdot ... \cdot (n - k + 1)}{k!}\]
(vgl. Merkhilfe)
Insgesamt interessieren sich 12 Stadträtinnen und Stadträte für einen der 3 zu vergebenden Sitze.
Es gibt \(\displaystyle \binom{12}{3}\) Möglichkeiten, die 3 Sitze mit 3 von 12 Stadrätinnen und Stadträten zu besetzen.
Berechnung der Wahrscheinlichkeit \(P(X = 1)\)
Es gibt \(\displaystyle \binom{8}{1}\) Möglichkeiten, einen der drei Sitze mit einer der 8 Stadträtinnen zu besetzen.
Es verbleiben \(\displaystyle \binom{4}{2}\) Möglichkeiten, die übrigen Sitze mit 2 der 4 Stadträte zu besetzen.
\[P(X = 1) = \frac{\displaystyle \binom{8}{1} \cdot \binom{4}{2}}{\displaystyle \binom{12}{3}} = \frac{12}{55}\]
Berechnung der Wahrscheinlichkeit \(P(X = 2)\)
Es gibt \(\displaystyle \binom{8}{2}\) Möglichkeiten, zwei der drei Sitze mit 2 der 8 Stadträtinnen zu besetzen.
Es verbleiben \(\displaystyle \binom{4}{1}\) Möglichkeiten, den übrigen Sitz mit einem der 4 Stadträte zu besetzen.
\[P(X = 2) = \frac{\displaystyle \binom{8}{2} \cdot \binom{4}{1}}{\displaystyle \binom{12}{3}} = \frac{28}{55}\]
2. Lösungsansatz: Baumdiagramm
Betrachtet werden folgende Ereignisse:
♂ : „Stadtrat erhält einen Sitz"
♀ : „Stadträtin erhält einen Sitz"
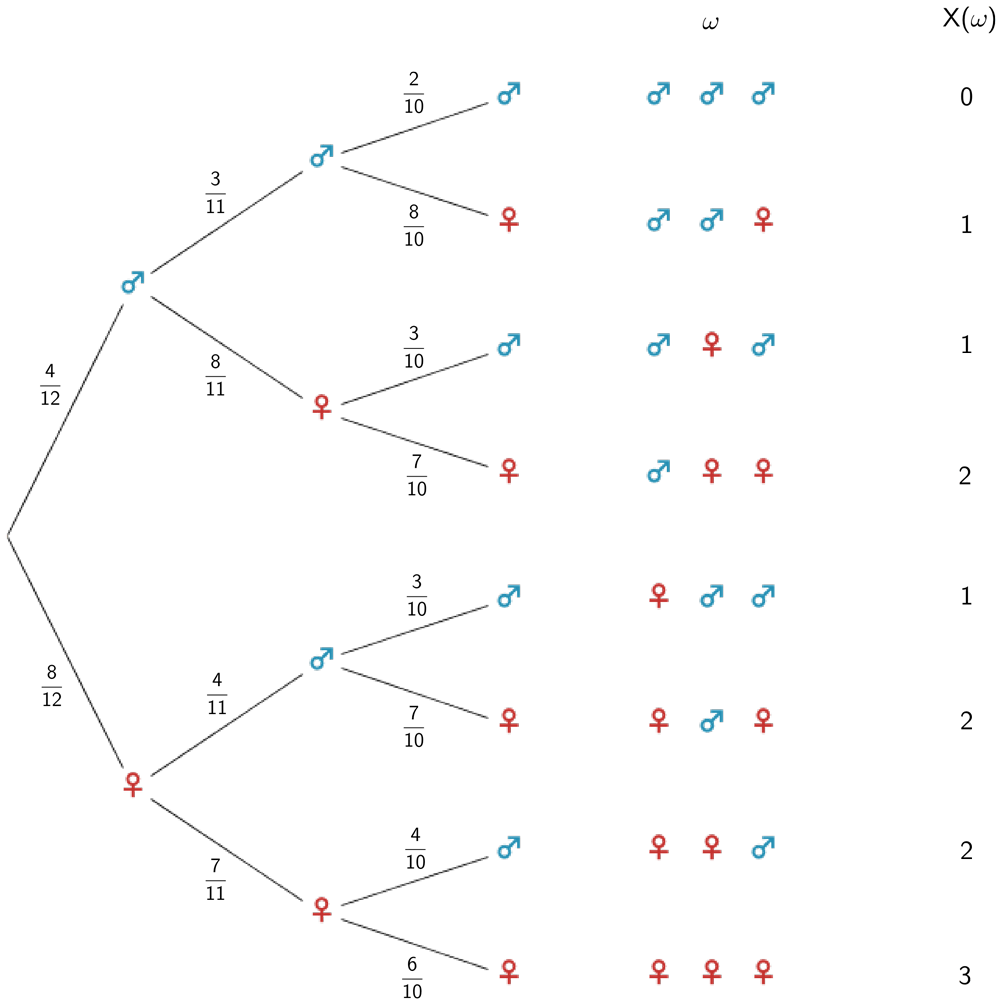
Baumdiagramm für die Ereignisse ♂ : „Stadtrat erhält einen Sitz" und ♀ : „Stadträtin erhält einen Sitz"
Da die Lose für einen der drei Sitze einmalig vergeben werden, verändern sich die Wahscheinlichkeiten für die Ereignisse ♂ und ♀ von einer Stufe zur nächsten.
Anwenden der 1. und der 2. Pfadregel:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(X = 1) &= P(\{\textcolor{#248fb3}{♂} \; \textcolor{#248fb3}{♂} \; \textcolor{#c4312e}{♀}\}) + P(\{\textcolor{#248fb3}{♂} \; \textcolor{#c4312e}{♀} \; \textcolor{#248fb3}{♂}\}) + P(\{\textcolor{#c4312e}{♀} \; \textcolor{#248fb3}{♂} \; \textcolor{#248fb3}{♂}\}) \\[0.8em] &=\frac{4}{12} \cdot \frac{3}{11} \cdot \frac{8}{10} + \frac{4}{12} \cdot \frac{8}{11} \cdot \frac{3}{10} + \frac{8}{12} \cdot \frac{4}{11} \cdot \frac{3}{10} \\[0.8em] &= \frac{288}{1320} \\[0.8em] &= \frac{12}{55}\end{align*}\]
\[\begin{align*}P(X = 2) &= P(\{\textcolor{#248fb3}{♂} \; \textcolor{#c4312e}{♀} \; \textcolor{#c4312e}{♀}\}) + P(\{\textcolor{#c4312e}{♀} \; \textcolor{#248fb3}{♂} \; \textcolor{#c4312e}{♀}\}) + P(\{\textcolor{#c4312e}{♀} \; \textcolor{#c4312e}{♀} \; \textcolor{#248fb3}{♂}\}) \\[0.8em] &=\frac{4}{12} \cdot \frac{8}{11} \cdot \frac{7}{10} + \frac{8}{12} \cdot \frac{4}{11} \cdot \frac{7}{10} + \frac{8}{12} \cdot \frac{7}{11} \cdot \frac{4}{10} \\[0.8em] &= \frac{672}{1320} \\[0.8em] &= \frac{28}{55}\end{align*}\]
