Gegeben ist eine in \(\mathbb R\) definierte ganzrationale Funktion \(f\) dritten Grades, deren Graph \(G_{f}\) an der Stelle \(x = 1\) einen Hochpunkt und an der Stelle \(x = 4\) einen Tiefpunkt besitzt.
Begründen Sie, dass der Graph der Ableitungsfunktion \(f'\) von \(f\) eine Parabel ist, welche die \(x\)-Achse in den Punkten \((1|0)\) und \((4|0)\) schneidet und nach oben geöffnet ist.
(3 BE)
Lösung zu Teilaufgabe 4a
Graph der Ableitung einer Funktion beschreiben
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
Gemäß der Ableitungsregel einer Potenzfunktion sowie der Faktor- und der Summenregel ist die Ableitung einer ganzrationalen Funktion \(n\)-ten Grades eine ganzrationale Funktion vom Grad \(n - 1\).
Die Ableitung \(f'\) einer ganzrationalen Funktion \(f\) dritten Grades ist demnach eine ganzrationale Funktion zweiten Grades (quadratische Funktion), deren Graph eine Parabel ist.
\[f(x) = ax^{3} + bx^{2} + cx + d\]
\[\Longrightarrow \quad f'(x) = 3ax^{2} + 2bx + c\]
\(\Longrightarrow \quad G_{f'}\) ist eine Parabel.
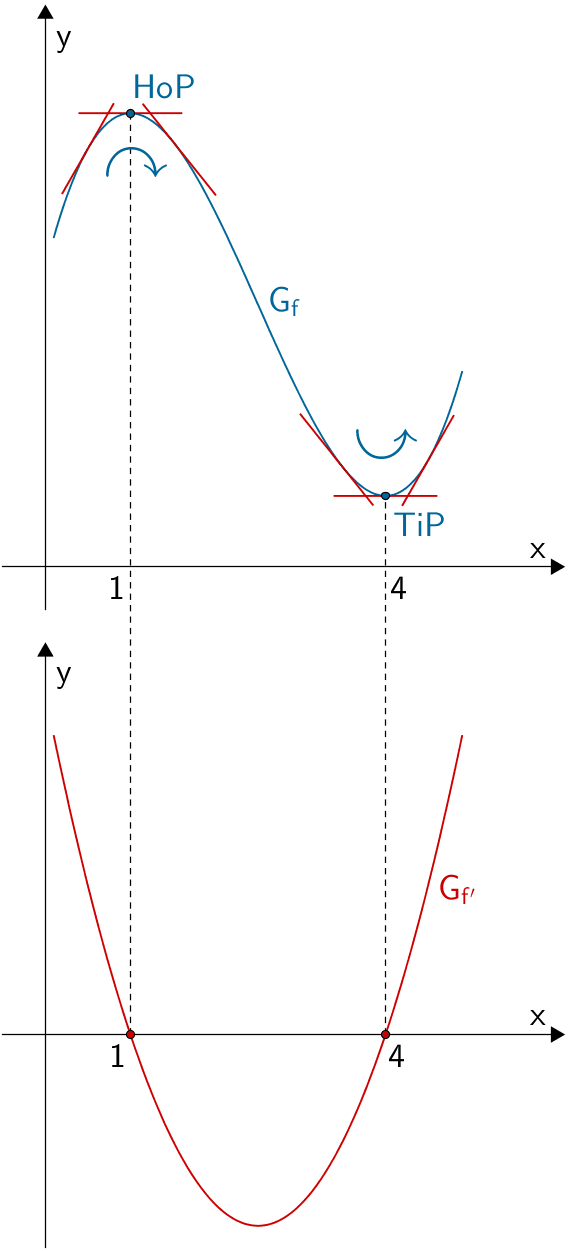
Der Graph der Funktion \(f\) hat an den Extremstellen \(x = 1\) und \(x = 4\) eine waagrechte Tangente (Tangentensteigung ist gleich Null). Da die erste Ableitung einer Funktion die Steigung der Tangente an den Graphen der Funktion beschreibt, gilt an den Extremstellen: \(f'(1) = 0\) bzw. \(f'(4) = 0\) (Notwendige Bedingung für eine Extremstelle). Folglich schneidet die Parabel die \(x\)-Achse in den Punkten \((1|0)\) und \((4|0)\).
In der Umgebung des Hochpunkts \((HoP)\) wechselt die Steigung einer Tangente an \(G_f\) von \(+\) nach \(-\) und in der Umgebung des Tiefpunkts \((TiP)\) wechselt die Steigung einer Tangente an \(G_{f}\) von \(-\) nach \(+\). Also hat \(f'\) für \(x = 1\) eine einfache Nullstelle mit Vorzeichenwechsel von \(+\) nach \(-\) und für \(x = 4\) eine einfache Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\). Folglich fällt die Parabel von \(f'\) in der Umgebung von \(x = 1\) streng monoton und steigt in der Umgebung von \(x = 4\) streng monoton, was den Verlauf einer nach oben geöffneten Parabel bestätigt.
Alternative Begründung mithilfe der Graphenkrümmung:
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
In der Umgebung des Hochpunkts \((HoP)\) ist \(G_{f}\) rechtsgekrümmt und es gilt \(f''(x) < 0\). In der Umgebung des Tiefpunkts \((TiP)\) ist \(G_{f}\) linksgekrümmt und es gilt \(f''(x) > 0\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Die zweite Ableitung einer Funktion beschreibt die Steigung der Tangente an den Graphen der ersten Ableitung der Funktion. Wendet man das Monotoniekriterium auf die zweite Ableitung an, so lässt sich aus dem Vorzeichen von \(f''\) schlussfolgern, dass die Parabel von \(f'\) in der Umgebung von \(x = 1\) streng monoton fällt und in der Umgebung von \(x = 4\) streng monoton steigt. Folglich ist die Parabel nach oben geöffnet.

