Allgemeine Sinus- und Kosinusfunktion
Eine Funktion \(f\) mit \(f(x) = a \cdot \sin(bx + c) + d\) bzw. \(f(x) = a \cdot \cos(bx + c) + d\) und \(a, b, c, d \in \mathbb R\) sowie \(a \neq 0, b \neq 0\) heißt allgemeine Sinus- bzw. Kosinusfunktion (\(x\): Winkel im Bogenmaß).
Die Parameter \(a, b, c\) und \(d\) bestimmen die Entstehung des Graphen einer allgemeinen Sinus- bzw. Kosinusfunktion, ausgehend von den Graphen der Grundfunktionen \(x \mapsto \sin x\) und \(x \mapsto \cos x\) (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
Parameter \(a\):
Bestimmt die Amplitude, d.h. den Maximalausschlag nach oben oder unten um \(\vert a \vert\). Entspricht einer Streckung um \(a\) in \(y\)-Richtung.
Parameter \(b\):
Bestimmt die Periode, d.h. die „Länge für eine Schwingung". Es gilt: \(p = \frac{2\pi}{\vert b \vert}\). Entspricht einer Streckung um \(\frac{1}{b}\) in \(x\)-Richtung.
Parameter \(c\):
Bestimmt die Phasenverschiebung, d.h. die Verschiebung längs der \(x\)-Achse.
Parameter \(d\):
Bestimmt die Verschiebung längs der \(y\)-Achse.
Um die resultierende Verschiebung durch die Parameter \(b\) und \(c\) des Graphen einer allgemeinen Sinus- bzw. Kosinusfunktion bzgl. des Graphen der Grundfunktion \(x \mapsto \sin x\) bzw. \(x \mapsto \cos x\) zu ermitteln, formt man den Funktionsterm um:
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin\left[b \left(x + \dfrac{b}{c}\right)\right] + d\]
\[f(x) = a \cdot \cos(bx + c) + d = a \cdot \cos\left[b \left(x + \dfrac{b}{c} \right)\right] + d\]
\(\Longrightarrow \quad\)Verschiebung um \(-\frac{c}{b}\) in \(x\)-Richtung bezgl. der Graphen der Funktionen \(x \mapsto \sin x\) bzw. \(x \mapsto \cos x\)
Definitionsbereich: \(D_{f} = R\)
Wertebereich: \(W_{f} = [-a;+a]\) für \(d = 0\) bzw. \(W_{f} = [d - a;d + a]\) für \(d \neq 0\)
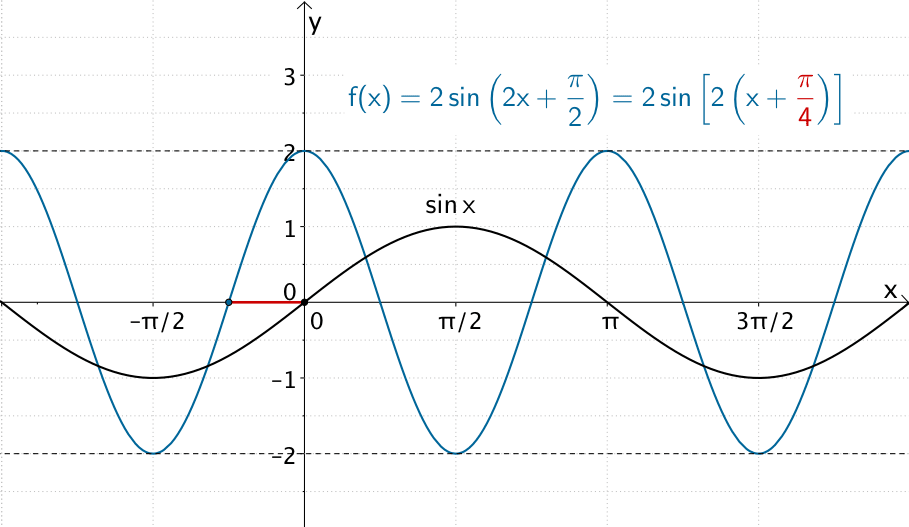
Der Graph der allgemeinen Sinusfunktion \(f\colon x \mapsto 2\sin\left( 2x + \frac{\pi}{2} \right)\) mit der Amplitude \(a = 2\) hat den Wertebereich \(W_{f} = [-2;2]\) und ist gegenüber der Sinusfunktion \(x \mapsto \sin x\) um \(-\frac{c}{b} = -\frac{\pi}{4}\) in \(x\)-Richtung verschoben.
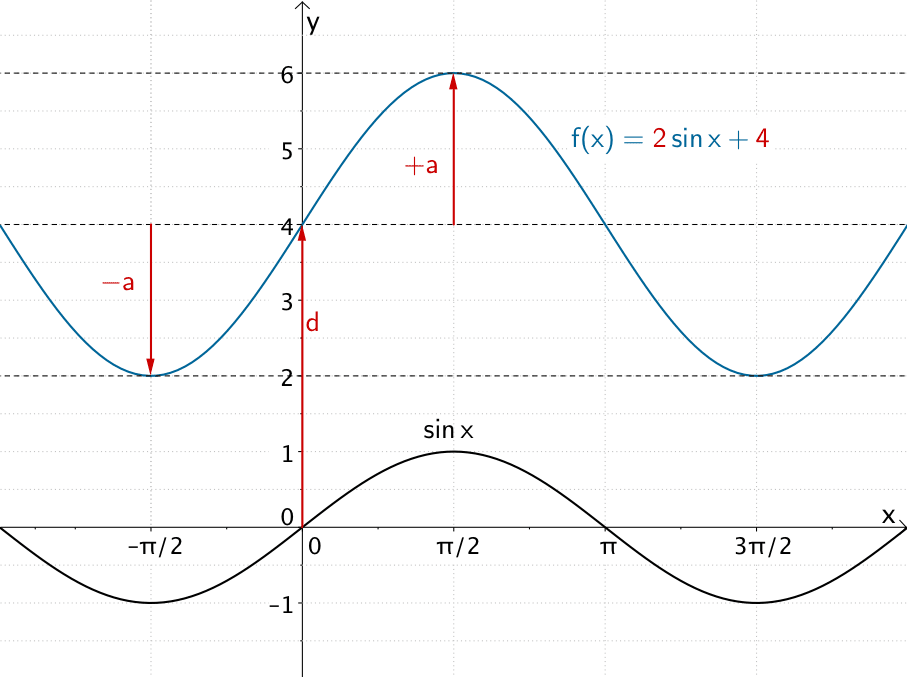
Der Graph der allgemeinen Sinusfunktion \(f \colon x \mapsto 2 \sin x + 4\) mit der Amplitude \(a = 2\) ist gegenüber der Sinusfunktion \(x \mapsto \sin x\) um \(d = 4\) in \(y\)-Richtung verschoben und hat den Wertebereich \(W_{f} = [d - a; d + a] = [2;6]\).
Eigenschaften der Sinusfunktion \(x \mapsto \sin x\) und der Kosinusfunktion \(x \mapsto \cos x\)
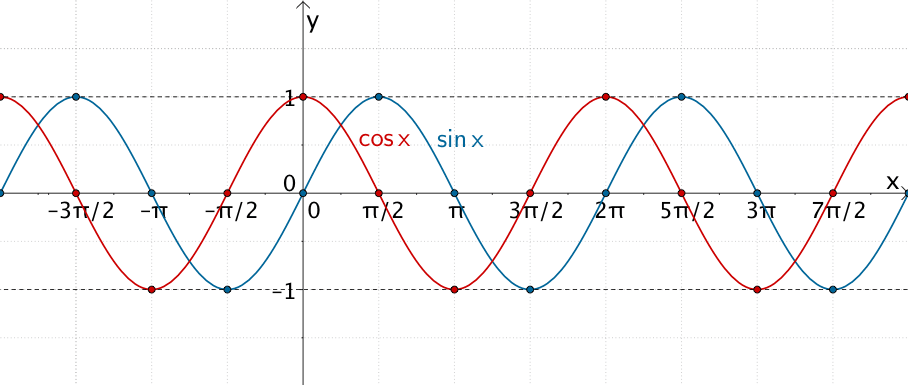
Graph der Sinusfunktion \(x \mapsto \sin x\) und Graph der Kosinusfunktion \(x \mapsto \cos x\)
| Eigenschaften (\(k \in \mathbb Z\)) | \(f(x) = \sin x\) | \(f(x) = \cos x\) |
| Definitionsbereich | \(D_{f} = \mathbb R\) | \(D_{f} = \mathbb R\) |
| Wertebereich | \(W_{f} = [-1;1]\) | \(W_{f} = [-1;1]\) |
| Periode | \(2\pi\) | \(2\pi\) |
| Symmetrieverhalten | punktsymmetrisch zum Ursprung | achsensymmetrisch zur \(y\)-Achse |
| Nullstellen | \(x = k \cdot \pi\) | \(x = \dfrac{\pi}{2} + k \cdot \pi\) |
| Relative Maxima | \(x = \dfrac{\pi}{2} + k \cdot 2\pi\) | \(x = k \cdot 2\pi\) |
| Relative Minima | \(x = \dfrac{3}{2}\pi + k \cdot 2\pi\) | \(x = \pi + k \cdot 2\pi\) |
Beziehungen zwischen den trigonometrischen Funktionen
Nachfolgend sei eine Auswahl häufig auftretender trigonometrischer Beziehungen genannt.
Der Graph der Kosinusfunktion läuft dem Graphen der Sinusfunktion um \(\frac{\pi}{2}\) voraus, d.h der Graph der Kosinusfunktion entsteht aus dem Graphen der Sinusfunktion durch Verschiebung um \(-\frac{\pi}{2}\) in \(x\)-Richtung.
Der Graph der Sinusfunktion läuft dem Graphen der Kosinusfunktion um \(\frac{\pi}{2}\) hinterher, d.h. der Graph der Sinusfunktion entsteht aus dem Graphe der Kosinusfunktion durch Verschiebung um \(+\frac{\pi}{2}\) in \(x\)-Richtung.
Beziehung zwischen der Sinusfunktion und der Kosinusfunktion
\[\cos x = \sin \left(x + \frac{\pi}{2} \right)\]
\[\sin x = \cos \left(x - \frac{\pi}{2} \right)\]
Trigonometrischer Pythagoras
\[(\sin x)^{2} + (\cos x)^{2} = \sin^{2}x + \cos^{2}x = 1\]
Tangensfunktion
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 3 \cdot \sin\left( \frac{2}{3}x + \pi \right)\). Bestimmen Sie für \(x \in \; ]-\frac{3}{2}\pi;3\pi[\) die Nullstellen von \(f\).
\[f(x) = 3 \cdot \sin\left( \dfrac{2}{3}x + \pi \right)\,; \enspace D = \mathbb R\]
\[\begin{align*} f(x) &= 0 \\[0.8em] 3\cdot \sin\left( \dfrac{2}{3}x + \pi \right) &= 0 & &| : 3 \\[0.8em] \sin\left( \dfrac{2}{3}x + \pi \right) &= 0 \end{align*}\]
Nullstellen der Sinusfunktion \(x \mapsto \sin x\):
\[x = k \cdot \pi\,, \enspace k \in \mathbb Z\]
Damit ergibt sich folgende Bedingung für die Nullstellen der Funktion \(f\):
\[\begin{align*} \Longrightarrow \quad \frac{2}{3}x + \pi &= k \cdot \pi & &| - \pi \\[0.8em] \frac{2}{3}x &= k \cdot \pi - \pi & &| \cdot \frac{3}{2} \\[0.8em] x &= \frac{3}{2} \cdot \left(k \cdot \pi - \pi \right) \\[0.8em] x&= k \cdot \frac{3}{2}\pi - \frac{3}{2}\pi \end{align*}\]
Nullstellen für \(x \in \: ]-\frac{3}{2}\pi;3\pi[\) mit \(k \in \mathbb Z\) berechnen:
\[\begin{align*}k = 0 \colon \quad x_{0} &= 0 \cdot \frac{3}{2}\pi - \frac{3}{2}\pi = - \frac{3}{2}\pi & & \Longrightarrow \quad x \notin \: ]-\frac{3}{2}\pi;3\pi[ \\[0.8em] k = 1 \colon \quad x_{1} &= 1 \cdot \frac{3}{2}\pi - \frac{3}{2}\pi = 0 & & \Longrightarrow \quad x \in \: ]-\frac{3}{2}\pi;3\pi[ \\[0.8em] k = 2 \colon \quad x_{2} &= 2 \cdot \frac{3}{2}\pi - \frac{3}{2}\pi = \frac{3}{2}\pi & & \Longrightarrow \quad x \in \: ]-\frac{3}{2}\pi;3\pi[ \\[0.8em] k = 3 \colon \quad x_{3} &= 3 \cdot \frac{3}{2}\pi - \frac{3}{2}\pi = 3\pi & & \Longrightarrow \quad x \notin \: ]-\frac{3}{2}\pi;3\pi[ \end{align*}\]
Für \(x \in \: ]-\frac{3}{2}\pi;3\pi[\) besitzt die Funktion \(f\) die beiden Nullstellen \(x_{1} = 0\) und \(x_{2} = \frac{3}{2}\pi\).
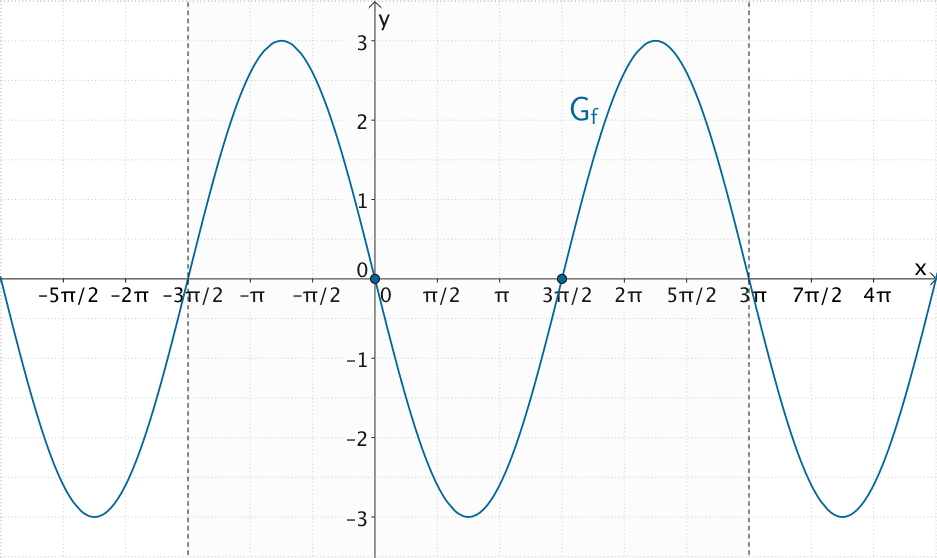
Graph der Funktion \(f\colon x \mapsto 3 \cdot \sin\left( \frac{2}{3}x + \pi \right)\) mit Nullstellen \(x_{1} = 0\) und \(x_{2} = \frac{3}{2}\pi\) für \(x \in \;]-\frac{3}{2}\pi;3\pi[\)


