Bestimmen Sie den Funktionswert von \(f\) an der Stelle 1; veranschaulichen Sie Ihr Vorgehen in Abbildung 1.
(3 BE)
Lösung zu Teilaufgabe 2b
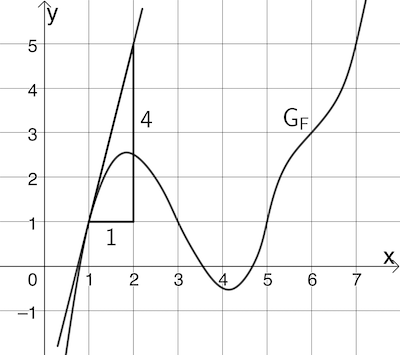Abb. 1
\[f(1) = F'(1) = 4\]
Ausführliche Erklärung (nicht verlangt)
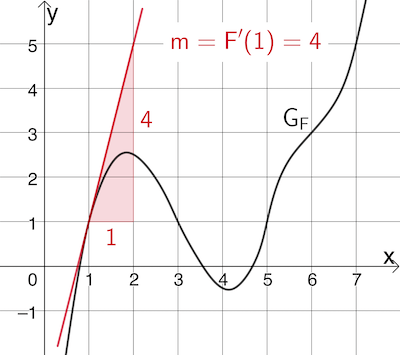Abb. 1
Abbildung 1 zeigt den Graphen \(G_F\) einer in \(\mathbb R\) definierten Stammfunktion \(F\) einer in \(\mathbb R\) definierten Funktion \(f\). Gemäß der Definition einer Stammfunktion gilt:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\[F'(x) = f(x)\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die Steigung \(\textcolor{#cc071e}{m}\) der Tangente an den Graphen der Stammfunktion \(F\) an der Stelle \(\textcolor{#cc071e}{x = 1}\) beschreibt den Wert der Ableitungsfunktion \(F'\) an der Stelle \(x = 1\), also den Funktionswert \(\textcolor{#cc071e}{F'(1)}\). Mithilfe eines Steigungsdreiecks ergibt sich: \(\textcolor{#cc071e}{m = F'(1) = 4}\).
Mit \(F'(x) = f(x)\) folgt:
\[f(1) = \textcolor{#cc071e}{F'(1) = 4}\]
