Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt \(A_{0}\) dem Wert des Integrals \(\displaystyle \int_{e}^{x_{S}} (x - h^{*}(x)) dx\) entspricht, wobei \(x_{S}\) die \(x\)-Koordinate von Punkt \(S\) ist. Der Graph von \(h^{*}\), der Graph der Umkehrfunktion von \(h^{*}\) sowie die beiden Koordinatenachsen schließen im ersten Quadranten ein Flächenstück mit Inhalt \(A\) ein. Geben Sie unter Verwendung von \(A_{0}\) einen Term zur Berechnung von \(A\) an.

(4 BE)

Lösung zu Teilaufgabe 1f

 

Bestimmtes Integral, Flächeninhalt zwischen zwei Funktionsgraphen

 

\[A_{0} = \int_{e}^{x_{S}} \left( x - h^{*}(x) \right) dx\]

 

Flächenstück mit dem Inhalt \(A_{0}\)

 

Der Wert des Integrals \(\displaystyle \int_{e}^{x_{S}} \left( x - h^{*}(x) \right) dx\) entspricht dem Inhalt \(A_{0}\) des Flächenstücks, das die Winkelhalbierende \(w \colon y = x\) des ersten und dritten Quadranten und der Graph der Funktion \(h^{*}\) im Intervall \([e;x_{S}]\) einschließen.

 

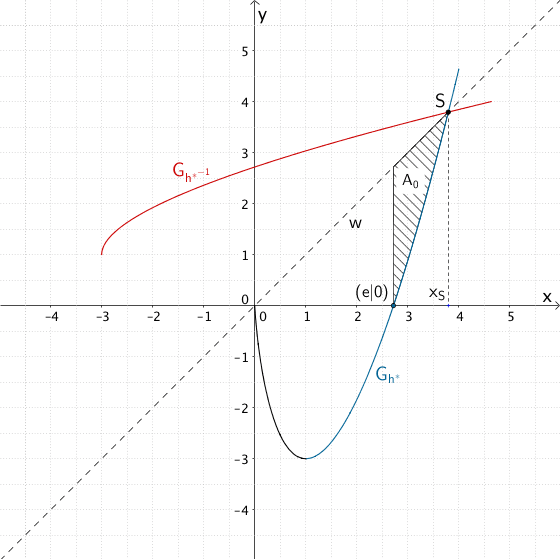
Flächeninhalt A₀, des Flächenstücks, das die Winkelhalbierende w und der Graph der Funktion h* zwischen x = e und der x-Koordinate des Punktes S einschließen

Flächeninhalt \(A_{0}\) des Flächenstücks, das die Winkelhalbierende \(w \colon y = x\) und der Graph der Funktion \(h^{*}\) im Intervall \([e;x_{S}]\) einschließen.

 

Term zur Berechnung von \(A\) unter Verwendung von \(A_{0}\)

 

Anmerkung:

Der Term zur Berechnung von \(A\) unter Verwendung von \(A_{0}\) ist lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.

 

Flächeninhalt A des Flächenstücks, das der Graph der Funktion h*, der Graph der Umkehrfunktion von h* sowie die beiden Koordinatenachsen im I. Quadranten einschließen.

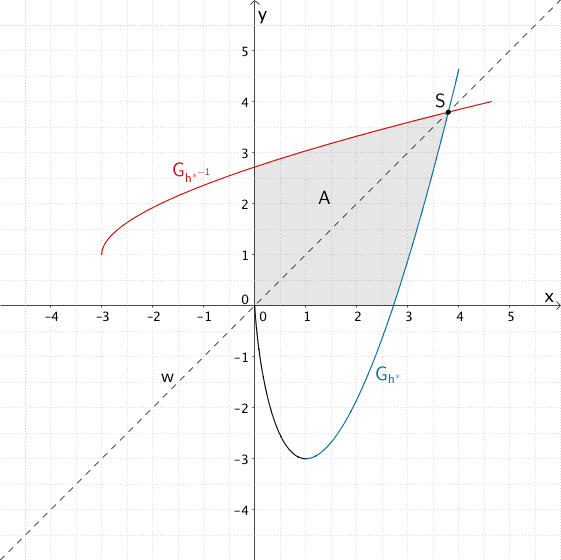
Die Winkelhalbierende \(w\) teilt das Flächenstück mit dem Flächeninhalt \(A\), das der Graph der Funktion \(h^{*}\), der Graph der Umkehrfunktion von \(h^{*}\) sowie die beiden Koordinatenachsen im ersten Quadranten einschließen, in zwei flächeninhaltsgleiche Flächenstücke.

 

Flächenstück mit dem Flächeninhalt A₀ und Flächeninhalt des Dreieck, welches die Winkelhalbierende w im Intervall [0;e] mit der x-Achse einschließt

Der Koordinatenursprung \((0|0)\), der Punkt \((e|0)\) (vgl. Teilaufgabe 1a) und der Punkt \((e|e)\) auf der Winkelhalbierenden \(w \colon y = x\) schließen ein rechtwinkliges Dreieck mit dem Flächeninhalt \(A_{\triangle}\) ein.

 

Somit ergibt sich der Flächeninhalt \(A\) unter Verwendung von \(A_{0}\) zu:

 

\[\begin{align*} A &= 2 \cdot \left( A_{0} + A_{\triangle} \right) \\[0.8em] &= 2 \cdot \left( A_{0} + \frac{1}{2} \cdot e \cdot e  \right) \\[0.8em] &= 2 \cdot A_{0} + e^{2} \end{align*}\]