In der Vorderseite der Dachgaube befindet sich ein Fenster. Dem Fenster entspricht im Modell das Flächenstück, das der Graph der Funktion \(g\) mit \(g(x) = ax^4 + b\) und geeigneten Werten \(a,b \in \mathbb R\) mit der \(x\)-Achse einschließt (vgl. Abbildung 3).
Begründen Sie, dass a negativ und b positiv ist.
(2 BE)
Lösung zu Teilaufgabe 2b
\[g(x) = ax^4 + b; \; a,b \in \mathbb R\]
Begründung, dass \(a\) negativ ist
Der Parameter \(a\) der Funktion \(g\) lässt sich mit dem Öffnungsfaktor \(a\) einer Parabel einer quadratischen Funktion \(x \mapsto ax^2 + bx + c\) vergleichen. Für \(a < 0\) ist die Parabel nach unten geöffnet. Ebenso ist der Graph von \(g\) (Parabel 4. Ordnung) für \(a < 0\) nach unten geöffnet und nur dann hat der Graph von \(g\) einen absoluten Hochpunkt, der im Modell die Höhe des Fensters begrenzt.
Alternative Begründung:
Damit der Graph von \(g\) mit der \(x\)-Achse das Flächenstück einschließt, welches im Modell dem Fenster entspricht, muss dieser für \(x \to \pm \infty\) nach \(-\infty\) verlaufen. Dieses Verhalten bestimmt der Term \(ax^4\). Das heißt, es muss gelten:
\[\lim \limits_{x\,\to\,\pm\infty} g(x) = \lim \limits_{x\,\to\,\pm\infty} ax^4 = -\infty \; \Rightarrow \; a < 0\]
(vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Verhalten für \(x \to -\infty\) und \(x \to +\infty\))
Begründung, dass \(b\) positiv ist
Der Parameter \(b\) bewirkt eine Verschiebung des Graphen von \(x \mapsto ax^4\) mit \(a < 0\) in \(y\)-Richtung. Damit der Hochpunkt des Graphen von \(g\) oberhalb der \(x\)-Achse liegt, muss \(b > 0\) gelten.
oder
Da der Graph von \(g\) die \(y\)-Achse oberhalb der \(x\)-Achse schneidet, muss \(b > 0\) gelten.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
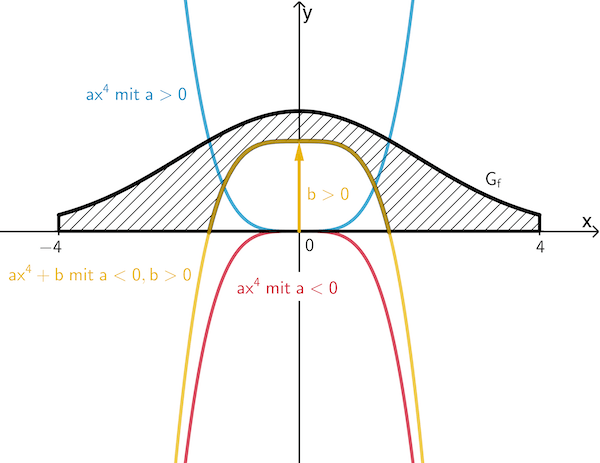
Einfluss der Parameter \(a\) und \(b\) auf den Verlauf des Graphen von \(g\colon x\mapsto ax^4 + b\) bezüglich der Modellierung des Fensters der Dachgaube (Skizze nicht verlangt)


