Abbildung 2 zeigt die Graphen von \(p\) und \(q\).
Welcher der beiden dargestellten Graphen ist \(G_g\,\)? Begründen Sie Ihre Antwort.
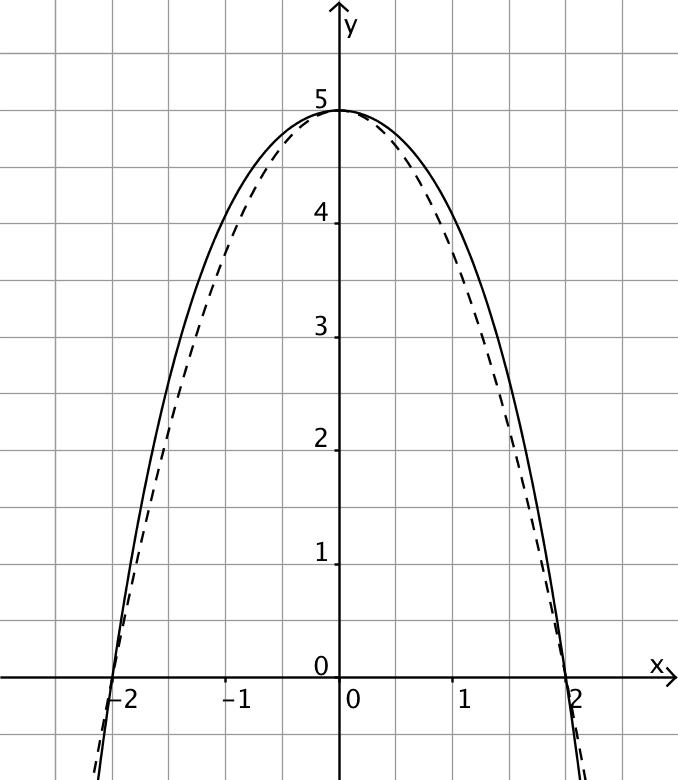 Abb. 2
Abb. 2
(2 BE)
Lösung zu Teilaufgabe 1c
1.Lösungansatz: Funktionswerte vergleichen
Wie Abb. 2 erkennen lässt, verläuft der in Strichlinie gezeichnete Graph für \(-2 < x < 0\) und \(0 < x < 2\) stets unterhalb des in Volllinie dargestellten Graphen. Folglich lassen sich die Graphen \(G_p\) und \(G_q\) durch einen Vergleich geeigneter Funktionswerte von \(p(x)\) und \(q(x)\) zuordnen.
\[p(x) = -1{,}25x^2 + 5\,; \quad D_p = \mathbb R\]
\[q(x) = -0{,}11x^4 - 0{,}81x^2 + 5 \,; \quad D_q = \mathbb R\]
\[p(1) = -1{,}25 \cdot 1^2 + 5 = 3{,}75\]
\[q(1) = -0{,}11 \cdot 1^4 - 0{,}81 \cdot 1^2 = 4{,}05\]
\[q(1) > p(1)\]
\(\Longrightarrow \quad\) Graph in Vollinie ist \(G_q\,\), Graph in Strichlinie ist \(G_p\)
2. Lösungsansatz: Differenzfunktion untersuchen
Differenzfunktion bilden:
\[x \in \; ]-2;0[\; \cup \; ]0;2[\]
\[\begin{align*}q(x) - p(x) &= -0{,}11x^4 - 0{,}81x^2 + 5 - \big( -1{,}25x^2 + 5 \big) \\[0.8em] &= -0{,}11x^4 + 0{,}44x^2 \\[0.8em] &= \underbrace{0{,}11x^2}_{>\,0}\big(\, \underbrace{4 - x^2}_{>\,0}\, \big) \end{align*}\]
\[\begin{align*} q(x) - p(x) &> 0 & &x \in \; ]-2;0[\; \cup \; ]0;2[ \\[0.8em] q(x) &> p(x) \end{align*}\]
\(\Longrightarrow \quad\) Graph in Vollinie ist \(G_q\,\), Graph in Strichlinie ist \(G_p\)
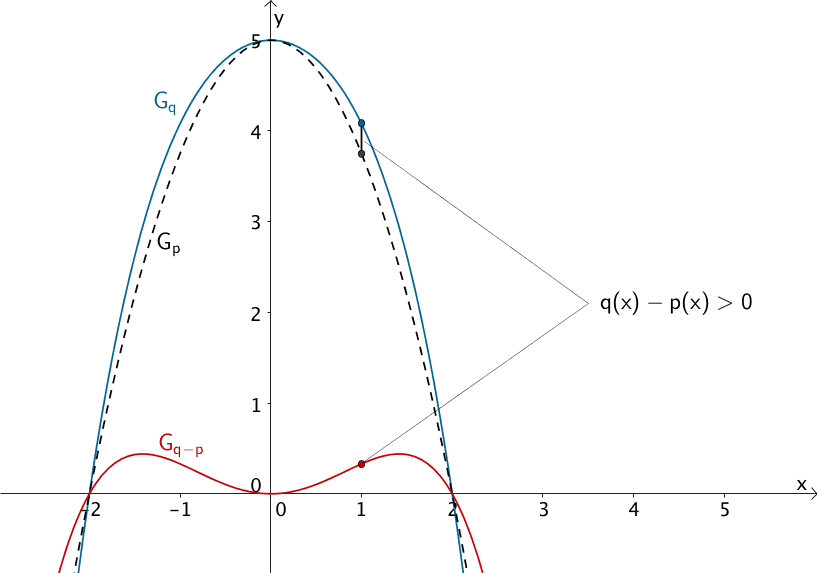
Für \(\,x \in \; ]-2;0[\; \cup \; ]0;2[\,\) ist der Wert der Differenzfunktion \(\,q(x) - p(x)\,\) stets gößer als Null.


