Gegeben ist die Funktion \(g \colon x \mapsto \ln(2x + 3)\) mit maximaler Definitionsmenge \(D\) und Wertemenge \(W\). Der Graph von \(g\) wird mit \(G_{g}\) bezeichnet.
Geben Sie \(D\) und \(W\) an.
(2 BE)
Lösung zu Teilaufgabe 1a
Definitionsmenge und Wertemenge einer Funktion
\[g(x) = \ln(2x + 3)\]
Maximale Definitionsmenge von \(g\)
Die (Natürliche) Logarithmusfunktion ist in \(\mathbb R^{+}\) definiert.
\[\begin{align*} 2x + 3 &> 0 & &| - 3 \\[0.8em] 2x &> -3 & &| : 2 \\[0.8em] x &> -\frac{3}{2} \end{align*}\]
\(\Longrightarrow \quad D = \; ] -\frac{3}{2}; +\infty[\)
Wertemenge von \(g\)
Es gilt: \(\lim \limits_{x \, \to \, 0} \ln{x} = -\infty\) und \(\lim \limits_{x \, \to \, +\infty} \ln{x} = +\infty\)
\[\left. \begin{align*} \lim \limits_{x \, \to \, -\frac{3}{2}} \ln(\underbrace{2x + 3}_{\to \, 0}) &= -\infty \\[0.8em] \lim \limits_{x \, \to \, +\infty} \ln(\underbrace{2x + 3}_{\to \, +\infty}) &= +\infty \end{align*} \right\} \enspace \Rightarrow \enspace W = \mathbb R\]
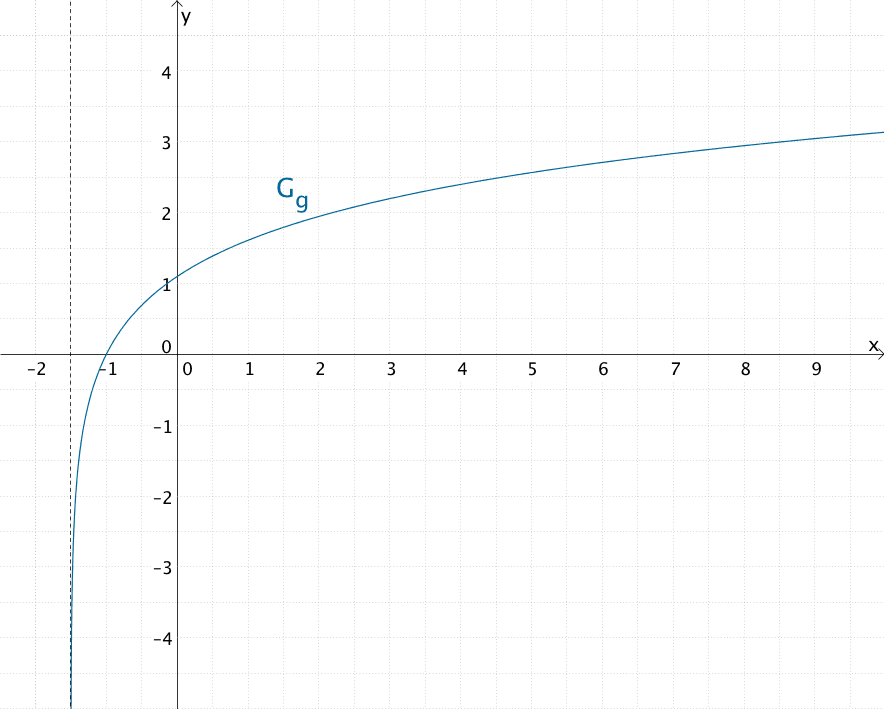
Verlauf des Graphen der Funktion \(g \colon x \mapsto \ln(2x + 3)\) mit Definitionsmenge \(D = \; ]-\frac{3}{2}; +\infty[\) und Wertemenge \(W = \mathbb R\)


