Berechnen Sie das Volumen des Körpers \(ABCDEF\).
(3 BE)
Lösung zu Teilaufgabe d
\[A_{\text{ABC}} = 6\cdot 6 - \frac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \frac{1}{2} \cdot 3 \cdot 6 = 13{,}5\]
\[V_{\text{ABCDEF}} = 13{,}5 \cdot 6 + \frac{1}{3} \cdot 13{,}5 \cdot 6 = 108\]
Das Volumen des Körpers \(ABCDEF\) beträgt 108 VE.
Ausführliche Lösung (nicht verlangt)
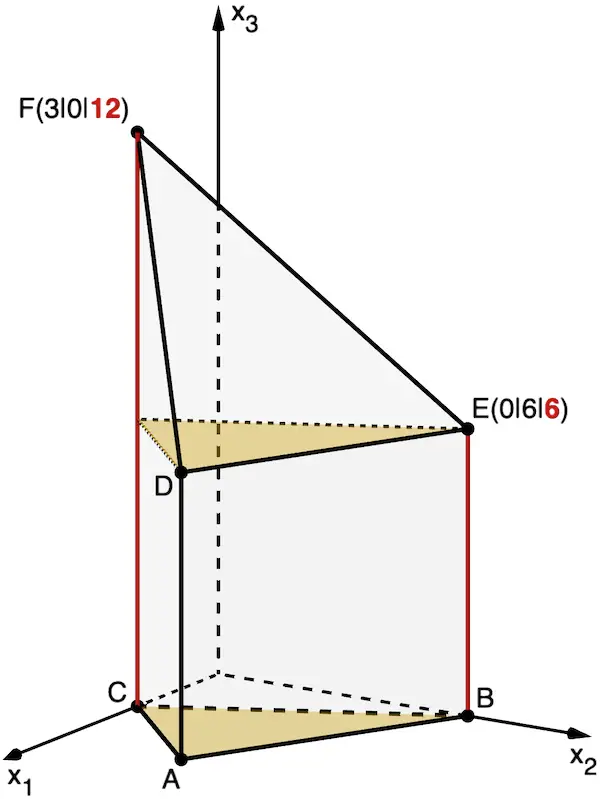
Planskizze (optional): Der Körper \(ABCDEF\) lässt sich in ein gerades Prisma mit der Grundfläche \(\textcolor{#e9b509}{ABC}\) und eine Pyramide mit der Spitze \(F\) zerlegen, deren Grundfläche die Deckfläche des Prismas ist.
Mithilfe des Terms aus Teilaufgabe c folgt:
\[\textcolor{#e9b509}{A_{\text{ABC}}} = 6\cdot 6 - \frac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \frac{1}{2} \cdot 3 \cdot 6 = \textcolor{#e9b509}{13{,}5}\]
Volumen eines geraden Prismas (vgl. Merkhilfe)
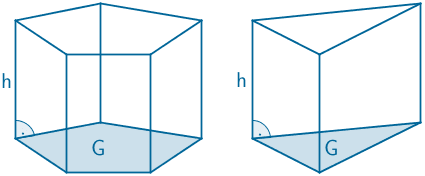
\[V_{\text{Prisma}} = G \cdot h\]
Die Höhe des Prismas ergibt sich beispielsweise aus der \(\textcolor{#cc071e}{x_3}\)-Koordinate des Punktes \(\textcolor{#cc071e}{E}\). Die Höhe der Pyramide entspricht dem Wert der Differenz der \(\textcolor{#cc071e}{x_3}\)-Koordinaten der Punkte \(\textcolor{#cc071e}{F}\) und \(\textcolor{#cc071e}{E}\).
\(\textcolor{#cc071e}{h_{\text{Prisma}} = x_{3_E} = 6}\)
\(\textcolor{#cc071e}{h_{\text{Pyramide}} = x_{3_F} - x_{3_E} = 12 - 6 = 6} \)
Volumen einer Pyramide
\[V = \frac{1}{3} \cdot G \cdot h\]
\(G\): Flächeninhalt der Grundfläche der Pyramide
\(h\): Höhe der Pyramide
(vgl. Merkhilfe)
\[\begin{align*}V_{\text{ABCDEF}} &= V_{\text{Prisma}} + V_{\text{Pyramide}} \\[0.8em] &= \textcolor{#e9b509}{G} \cdot \textcolor{#cc071e}{h} + \frac{1}{3} \cdot \textcolor{#e9b509}{G} \cdot \textcolor{#cc071e}{h} \\[0.8em] &= \textcolor{#e9b509}{13{,}5} \cdot \textcolor{#cc071e}{6} + \frac{1}{3} \cdot \textcolor{#e9b509}{13{,}5} \cdot \textcolor{#cc071e}{6} \\[0.8em] &= 13{,}5 \cdot 8 \\[0.8em] &= 108\end{align*}\]
Das Volumen des Körpers \(ABCDEF\) beträgt 108 VE (Volumeneinheiten).
