Die Punkte \(A(6|0|4)\), \(B(0|6|4)\), \(C(-6|0|4)\) und \(D\) liegen in der Ebene \(E\) und bilden die Eckpunkte der quadratischen Grundfläche einer Pyramide \(ABCDS\) mit der Spitze \(S(0|0|1)\). \(A\), \(B\) und \(S\) liegen in der Ebene \(F\).
Zeigen Sie rechnerisch, dass das Dreieck \(ABS\) gleichschenklig ist. Geben Sie die Koordinaten des Punkts \(D\) an und beschreiben Sie die besondere Lage der Ebene \(E\) im Koordinatensystem.
(4 BE)
Lösung zu Teilaufgabe a
Nachweis durch Rechnung, dass das Dreieck \(ABS\) gleichschenklig ist
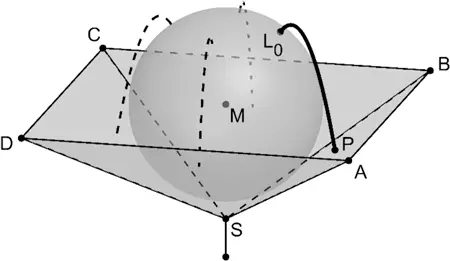
Die Abbildung lässt vermuten, dass \(ABCDS\) eine gerade Pyramide ist, deren Spitze \(S\) vertikal unter dem Schnittpunkt der Diagonalen der quadratischen Grundfläche \(ABCD\) liegt.
Es ist deshalb davon auszugehen, dass die Seiten \(\textcolor{#e9b509}{[SA]}\) und \(\textcolor{#e9b509}{[SB]}\) die gleichlangen Schenkel des Dreiecks \(ABS\) bilden.
\(A(6|0|4)\), \(B(0|6|4)\), \(S(0|0|1)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\textcolor{#e9b509}{\overline{SA}} &= \vert \overrightarrow{SA} \vert = \vert \overrightarrow{A} - \overrightarrow{S} \vert \\[0.8em] &= \left| \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| = \left| \begin{pmatrix} 6 \\ 0 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{6^{2} + 0^{2} + 3^{2}} = \textcolor{#e9b509}{3\sqrt{5}} \end{align*}\]
\[\begin{align*}\textcolor{#e9b509}{\overline{SB}} &= \vert \overrightarrow{SB} \vert = \vert \overrightarrow{B} - \overrightarrow{S} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 6 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| = \left| \begin{pmatrix} 0 \\ 6 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + 6^{2} + 3^{2}} = \textcolor{#e9b509}{3\sqrt{5}} \end{align*}\]
Somit ist \(ABS\) ein gleichschenkliges Dreieck mit der Basis \([AB]\).
Koordinaten des Punktes \(D\)
\[D(0|-6|4)\]
Begründung (nicht verlangt)
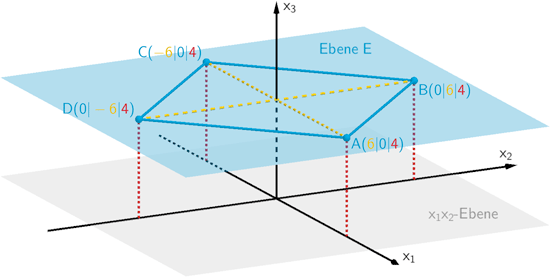
Die Punkte \(\textcolor{#0087c1}{A(\textcolor{#e9b509}{6}|0|\textcolor{#cc071e}{4})}\) und \(\textcolor{#0087c1}{C(\textcolor{#e9b509}{-6}|0|\textcolor{#cc071e}{4})}\) liegen im Abstand 4 vertikal über der \(x_{1}\)-Achse und haben von der \(x_{3}\)-Achse jeweils den Abstand 6.
Der Punkt \(\textcolor{#0087c1}{B(0|\textcolor{#e9b509}{6}|\textcolor{#cc071e}{4})}\) liegt im Abstand 4 vertikal über der \(x_{2}\)-Achse und hat von der \(x_{3}\)-Achse ebenfalls den Abstand 6.
Da die Punkte \(\textcolor{#0087c1}{A}\), \(\textcolor{#0087c1}{B}\), \(\textcolor{#0087c1}{C}\) und \(\textcolor{#0087c1}{D}\) in derselben Ebene \(\textcolor{#0087c1}{E}\) liegen und zudem die Diagonalen \(\textcolor{#e9b509}{[AC]}\) und \(\textcolor{#e9b509}{[BD]}\) der quadratischen Grundfläche \(ABCD\) gleichlang sind, folgt \(\textcolor{#0087c1}{D(0|\textcolor{#e9b509}{-6}|\textcolor{#cc071e}{4})}\).
Mögliche Begründung durch Rechnung:
Die Koordinaten des Punktes \(D\) lassen sich durch Vektoraddition bestimmen.
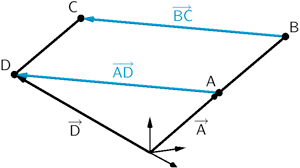
\(A(6|0|4)\), \(B(0|6|4)\), \(C(-6|0|4)\)
\[\begin{align*} \overrightarrow{D} &= \overrightarrow{A} + \textcolor{#0087c1}{\overrightarrow{AD}} &&| \; \textcolor{#0087c1}{\overrightarrow{AD}} = \textcolor{#0087c1}{\overrightarrow{BC}}\\[0.8em] &= \overrightarrow{A} + \textcolor{#0087c1}{\overrightarrow{BC}}\\[0.8em] &= \overrightarrow{A} + (\overrightarrow{C} - \overrightarrow{B}) \\[0.8em]&= \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} + \left[\begin{pmatrix}-6 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 6 \\ 4\end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 6 \\ 0 \\ 4 \end{pmatrix} + \begin{pmatrix}-6 \\ -6\\ 0 \end{pmatrix} \\[0.8em] &=\begin{pmatrix} 0 \\ -6 \\ 4 \end{pmatrix}\\[0.8em]&\Rightarrow \;D(0|-6|4)\end{align*}\]
Beschreibung der besonderen Lage der Ebene \(E\)
Da die \(x_{3}\)-Koordinate der in der Ebene \(E\) liegenden Punkte \(A\), \(B\), \(C\) und \(D\) gleich 4 ist, verläuft die Ebene \(E\) im Abstand 4 parallel zur \(x_{1}x_{2}\)-Ebene (vgl. Zeichnung oben).


