Gegeben ist die in \([-3;+\infty[\) definierte Funktion \(h \colon x \mapsto \sqrt{x+3}-2\).
Beschreiben Sie, wie der Graph von \(h\) aus dem Graphen der in \(\mathbb R_0^+\) definierten Funktion \(w \colon x \mapsto \sqrt{x}\) hervorgeht.
(2 BE)
Lösung zu Teilaufgabe 3a
\[h(x) = \sqrt{\textcolor{#e9b509}{x+3}}\textcolor{#cc071e}{-2}; \; D_h = [-3;+\infty[\]
\[w(x) = \sqrt{x}; \; D_w = \mathbb R_0^+\]
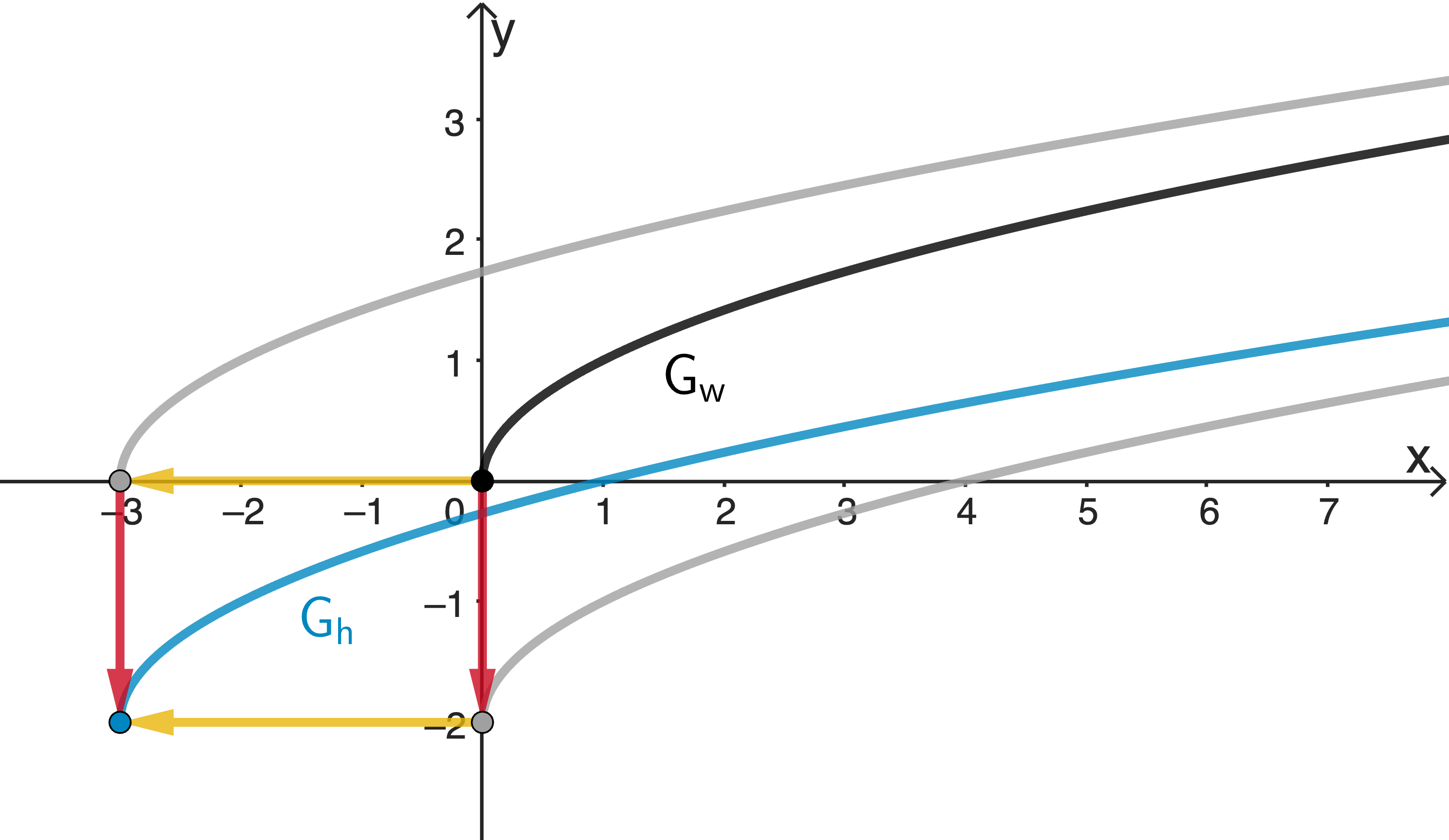ergänzende Skizze
Verschieben von Funktionsgraphen
\(g(x) = f(x +c) + d\) mit \(c,d \in \mathbb R\)
Verschieben um \(-c\) in \(x\)-Richtung
Verschieben um \(d\) in \(y\)-Richtung
Der Graph von \(h\) geht aus dem Graphen von \(w\) durch Verschiebung um 3 LE (Längeneinheiten) in negative \(\textcolor{#e9b509}{x}\)-Richtung und Verschiebung um 2 LE in negative \(\textcolor{#cc071e}{y}\)-Richtung hervor. Die Reihenfolge der beiden Schritte spielt dabei keine Rolle.
