Geben Sie einen möglichen Term der Funktion \(t\) an. Zeigen Sie für dieses \(t\) die Gültigkeit der Aussage aus Aufgabe 3a durch Integration mithilfe einer Stammfunktion.
(4 BE)
Lösung zu Teilaufgabe 3b
Es bietet sich an, eine Potenzfunktion ungerader Ordnung mit natürlichem Exponenten zu wählen, da die Stammfunktionen von Potenzfunktionen einfach zu bestimmen sind.
Es sei \(t\, \colon \; \mapsto x^3\,,\enspace x \in \mathbb R\) die Funktion \(t\), deren Graph \(G_t\) punktsymmetrisch zum Koordinatenursprung ist.
Nachweis der Punktsymmetrie:
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
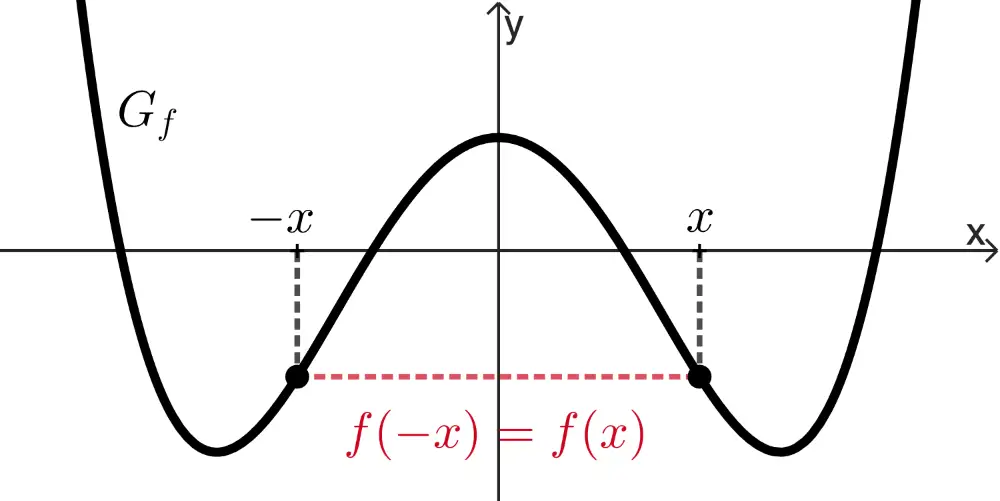
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
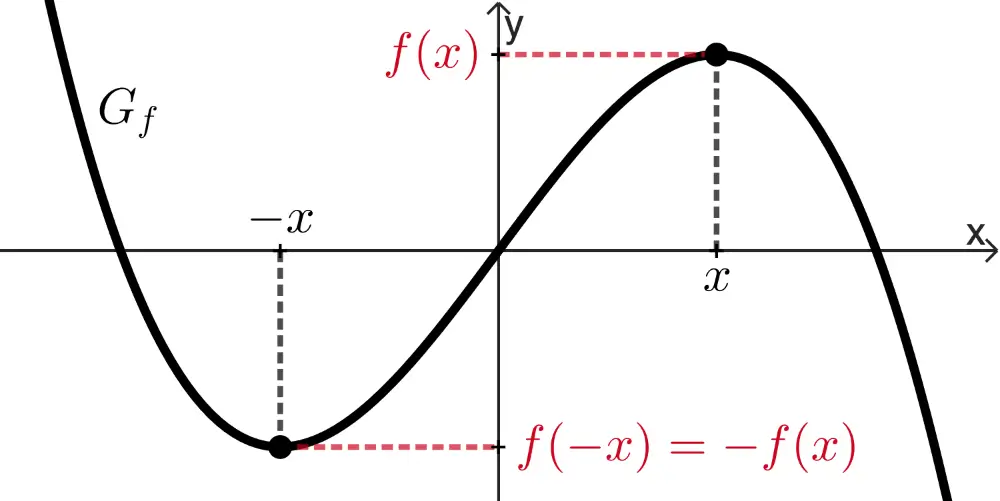
\(t(-x) = (-x)^3 = -x^3 = -t(x) \quad \Longrightarrow \quad\) \(G_t\) ist punktsymmetrisch zum Koordinatenursprung.
Stammfunktion \(T(x)\) bestimmen:
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[t(x) = x^3 \quad \Longrightarrow \quad T(x) = \frac{1}{4} x^4 + C\]
\(\Longrightarrow \quad\) Für \(C = 0\) ist \(T(x) = \frac{1}{4}x^4\) eine Stammfunktion von \(t(x)\).
Bestimmtes Integral berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[ \begin{align*} \int_{-a}^{a} x^3~dx &= \left [ \frac{1}{4}x^4 \right ]_{-a}^{a} \\[0.8em] &= \frac{1}{4}a^4 - \left ( \frac{1}{4} (-a)^4 \right ) \\[0.8em] &= \frac{1}{4}a^4 - \frac{1}{4} a^4 = 0 \end{align*}\]
![Bei der zum Koordinatenursprung punktsymmetrischen Funktion t(x) = x³ ist die Summe der Flächeninhalte, die der Graph von t im Intervall [-a; a] mit der x-Achse einschließt, gleich Null. Bei der zum Koordinatenursprung punktsymmetrischen Funktion t(x) = x³ ist die Summe der Flächeninhalte, die der Graph von t im Intervall [-a; a] mit der x-Achse einschließt, gleich Null.](/images/stories/B2014BA_PT_A_A_2/B2014BA_PT_A_A_2_3b.png)
Flächenbilanz des Graphen der zum Koordinatenursprung punktsymmetrischen Funktion \(t(x) = x^3\,\) im Intervall \([-a;a]\), \(a \in \mathbb R\): \(\displaystyle \;\int_{-a}^{a} x^3\;dx = 0\)


